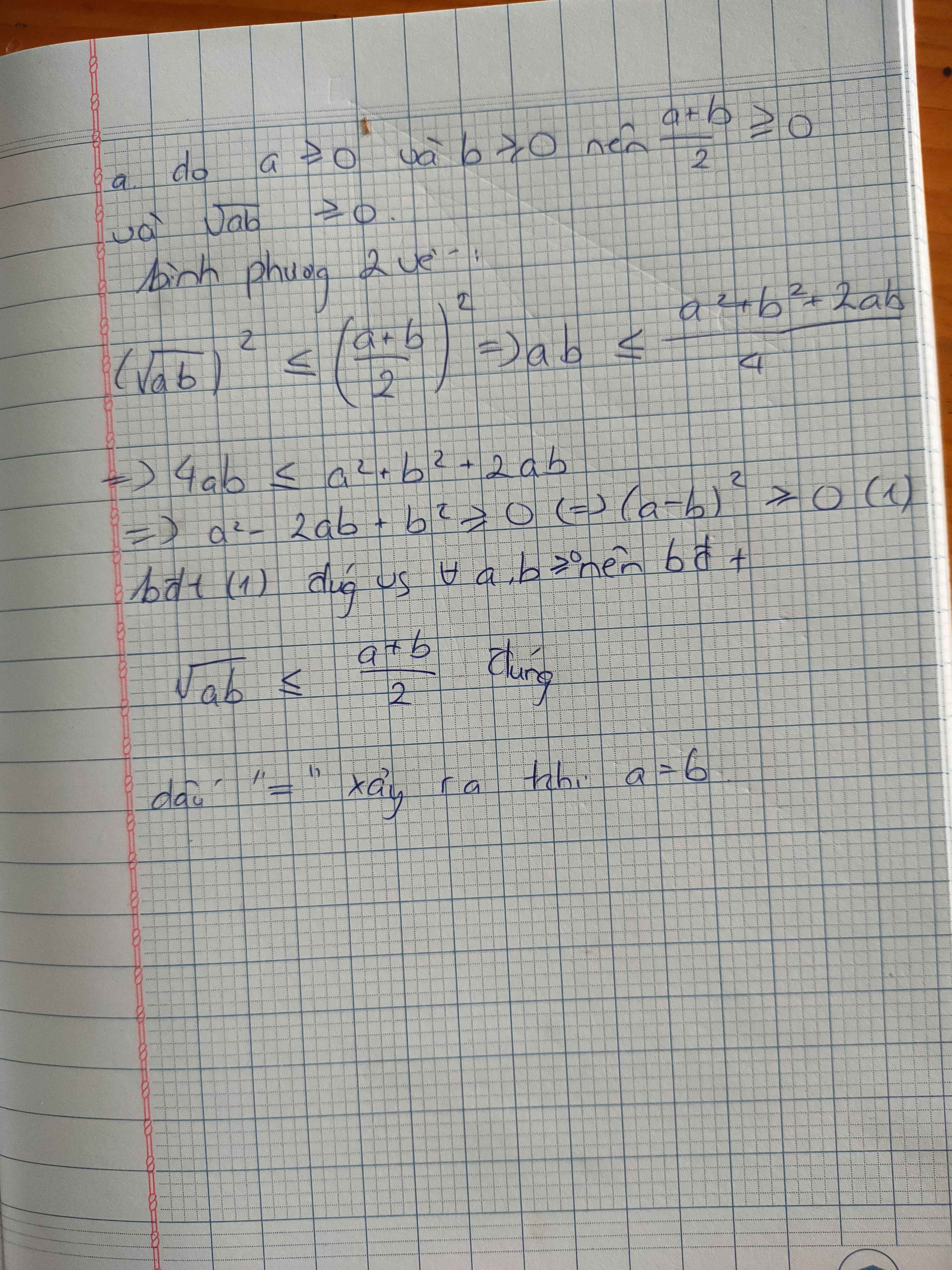a) Cho a ≥ 0, b ≥ 0. Chứng minh bất đẳng thức Cauchy: ![]()
b) Cho a, b, c > 0. Chứng minh rằng: ![]()
c) Cho a, b > 0 và 3a + 5b = 12. Tìm giá trị lớn nhất của tích P = a
Bài 2 :
Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
Bài 3:
hứng minh rằng không có giá trị nào của x, y, z thỏa mãn đẳng thức sau:
x2 + 4y2 + z2 – 2a + 8y – 6z + 15 = 0
Bài 4:ìm giá trị lớn nhất của biểu thức:![]()
bài 5:So sánh các số thực sau (không dùng máy tính):
~Gíup mik với nhé mik cần gấp~