ĐK: x≥0, x khác 1 Chứng minh rằng 0<A<2

Những câu hỏi liên quan
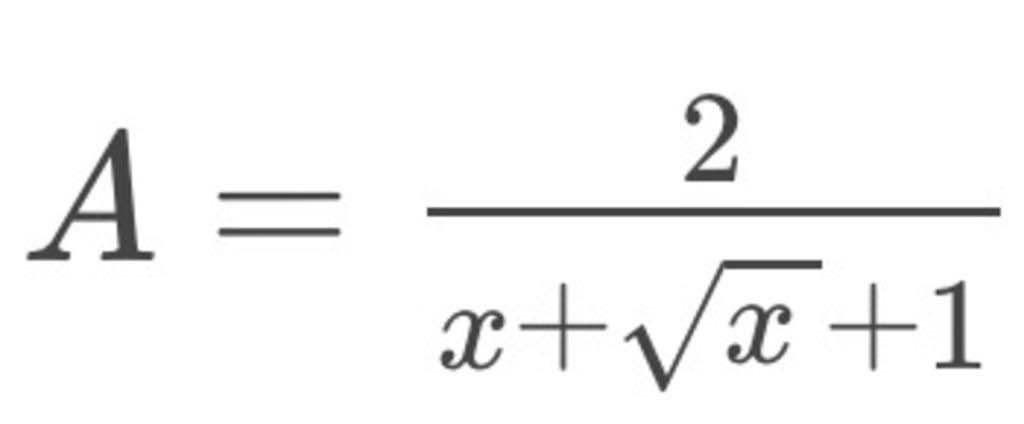 ĐK: x≥0, x khác 1
ĐK: x≥0, x khác 1
Chứng minh rằng 0<A<2
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
chứng minh rằng x0=1(x khác 0)
Ta có x0= 1 ( x khác 0)
Vì nó có định lý trong sgk toán
Đúng 0
Bình luận (0)
vì x0=1
mà theo tính chất x0=1
=> x\(\in\)N*
Đúng 0
Bình luận (0)
Với mọi giá trị x mà x0 thì luôn bằng
Ví dụ: 50 = 1; 260 = 1; ........
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
bài 1: M =(2-x-1/2x-3):(6x+1/2x^2-x-3+x/x+1)
đk(x>=0; x khác 3/2)
a, rút gọn M
b, chứng minh :M<3/2
cho biểu thức \(p=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}\) ĐK X>0;X KHÁC 1
RÚT GON P
TÍNH P KHI X=\(33-8\sqrt{2}\)
CHỨNG MINH RẰNG \(P< \frac{1}{3}\)
cho 3 số thực xyz khác 0 thoả mãn (x+y+z)^2=x^2+y^2+z^2 chứng minh rằng 1/x+1/y+1/z=0
(x+y+z)^2=x^2+y^2+z^2
=>2(xy+yz+xz)=0
=>xy+xz+yz=0
=>xy/xyz+xz/xyz+yz/xyz=0
=>1/x+1/y+1/z=0
Đúng 1
Bình luận (0)
1/x=1/2(1/y+1/z) (với x, y, z khác 0, x khác y), chứng minh rằng z/y=x-z/y-x
Ta có :\(\frac{1}{x}=\frac{1}{2}\left(\frac{1}{y}+\frac{1}{z}\right)\)
=> \(\frac{1}{x}=\frac{y+z}{2yz}\)
=> 2yz = x(y + z)
=> 2yz - xy - xz = 0
=> (yz - xy) + (yz - xz) = 0
=> y(z - x) + z(y- x) = 0
=> y(z - x) = -z(y - x)
=> -y(x - z) = -z(y - x)
=> \(\frac{-z}{-y}=\frac{x-z}{y-x}\Leftrightarrow\frac{z}{y}=\frac{x-z}{y-x}\)
Chứng minh rằng nếu x0 là nghiệm của P(x)=ax+b (a khác 0, b khác 0) thì 1/x0 là nghiệm của đa thức Q(x)=bx+a
P(x) = ax+ b = 0 =
=> ãx = -b => x = -b / a = x0
1/ x0 = 1/-b/a = a/-b thay vao Q(x) ta co
Q(x) = b. -a /b + a = -a + a = 0
Vậy x0 là nghiệm của P(x)=ax+b (a khác 0, b khác 0) thì 1/x0 là nghiệm của đa thức Q(x)=bx+a
Đúng 0
Bình luận (0)
Cho x, y, z khác 0, \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\). Chứng minh rằng: \(\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
Trước hết, ta đi chứng minh một bổ đề sau: Nếu \(a+b+c=0\) thì \(a^3+b^3+c^3=3abc\). Thật vậy, ta phân tích
\(P=a^3+b^3+c^3-3abc\)
\(P=\left(a+b\right)^3+c^3-3ab\left(a+b\right)-3abc\)
\(P=\left(a+b+c\right)\left[\left(a+b\right)^2+\left(a+b\right)c+c^2\right]-3ab\left(a+b+c\right)\)
\(P=\left(a+b+c\right)\left(a^2+b^2+c^2-ab-bc-ca\right)\).
Hiển nhiên nếu \(a+b+c=0\) thì \(P=0\) hay \(a^3+b^3+c^3=3abc\), bổ đề được chứng minh.
Do \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\) nên áp dụng bổ đề, ta được \(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}=\dfrac{3}{xyz}\).
Vì vậy \(\dfrac{yz}{x^2}+\dfrac{zx}{y^2}+\dfrac{xy}{z^2}=\dfrac{xyz}{x^3}+\dfrac{xyz}{y^3}+\dfrac{xyz}{z^3}\) \(=xyz\left(\dfrac{1}{x^3}+\dfrac{1}{y^3}+\dfrac{1}{z^3}\right)\) \(=xyz.\dfrac{3}{xyz}=3\). Ta có đpcm
Đúng 2
Bình luận (0)



















