Các câu hỏi tương tự
ĐK: x≥0, x khác 1 Chứng minh rằng 0<A<2
A=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\) và \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\) đk : x> 0; x khác 4
Cho P = A.B
Tìm GTNN của P
Cho a, b, c > 0 biết abc = 1
Chứng minh \(a^2+b^2+c^2\ge a+b+c\)
Cho P = \(\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}\) (đk x>-0 ; x khác 1/2 )
TÌM X BT |P| > HOẶC BẰNG P
Cho 2 biểu thức
A=2√x/x+3
B=√x+1/√x-3 +7√x+3/9+x
(đk x>= 0,x khác 9)
a)Tính giá trị tại của biểu thức A khi x=16
b) Rút gọn P=A+B
cho biểu thức \(p=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}\) ĐK X>0;X KHÁC 1
RÚT GON P
TÍNH P KHI X=\(33-8\sqrt{2}\)
CHỨNG MINH RẰNG \(P< \frac{1}{3}\)
Rút gọn:a, A √x√x−6−3√x+6+x36−xxx−6−3x+6+x36−x (đk: x ≥ 0 và x ≠ 36)b, B 9−x√x+3−x−6√x+9√x−3−69−xx+3−x−6x+9x−3−6 (đk: x ≥ 0 và x ≠ 9)c, C a+b(√a−√b)2−2√ab:(1√a−1√b)2a+b(a−b)2−2ab:(1a−1b)2 (đk: a 0, b 0 và a ≠ b)d, D (2−a√a2−√a+√a)(2−√a2−a)(2−aa2−a+a)(2−a2−a) (đk: a ≥ 0, a ≠ 2, a ≠ 4)
Đọc tiếp
Rút gọn:
a, A = √x√x−6−3√x+6+x36−xxx−6−3x+6+x36−x (đk: x ≥ 0 và x ≠ 36)
b, B = 9−x√x+3−x−6√x+9√x−3−69−xx+3−x−6x+9x−3−6 (đk: x ≥ 0 và x ≠ 9)
c, C = a+b(√a−√b)2−2√ab:(1√a−1√b)2a+b(a−b)2−2ab:(1a−1b)2 (đk: a > 0, b > 0 và a ≠ b)
d, D = (2−a√a2−√a+√a)(2−√a2−a)(2−aa2−a+a)(2−a2−a) (đk: a ≥ 0, a ≠ 2, a ≠ 4)
P= \(\dfrac{x+9}{6\sqrt{x}}\) đk x>0; x khác 4. Tìm GTNN của P
Cho hai phương trình ax2+bx+c=0(a khác 0) và mx2+nx+p=0 (m khác 0).Chứng minh rằng nếu ít nhất một trong hai phương trình trên vô nghiệm thì phương trình sau đây luôn có nghiệm (an-bm)x2 +2(ap-cm)x +bp-cn=0

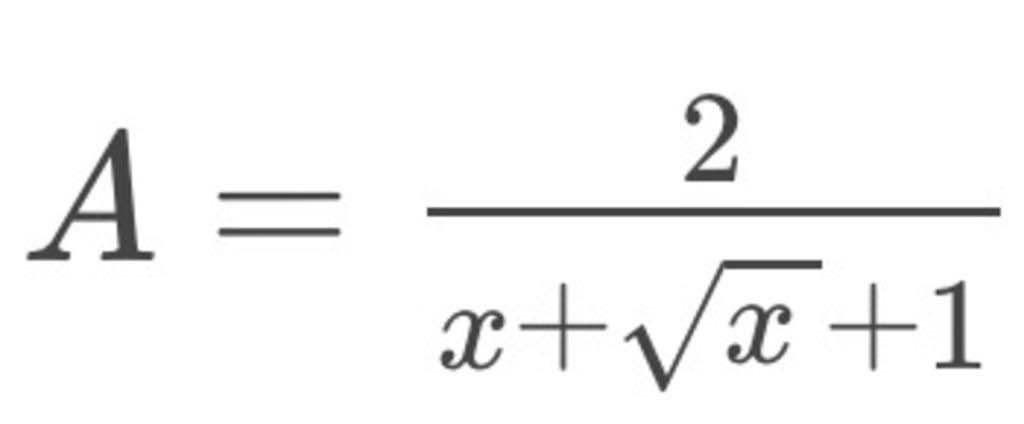 ĐK: x≥0, x khác 1
ĐK: x≥0, x khác 1





