Các câu hỏi tương tự
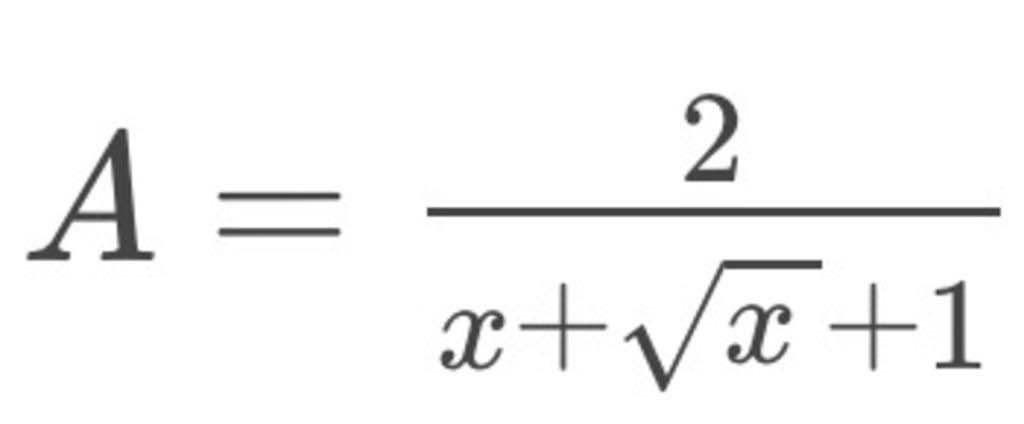ĐK: x≥0, x khác 1
Chứng minh rằng 0<A<2
cho biểu thức \(p=\frac{x+2}{x\sqrt{x}-1}+\frac{\sqrt{x}+1}{x+\sqrt{x}+1}-\frac{1}{\sqrt{x}-1}\) ĐK X>0;X KHÁC 1
RÚT GON P
TÍNH P KHI X=\(33-8\sqrt{2}\)
CHỨNG MINH RẰNG \(P< \frac{1}{3}\)
23 tháng 5 2023 lúc 13:38
Cho x, y, z khác 0, \(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}=0\). Chứng minh rằng: \(\dfrac{yz}{x^2}+\dfrac{xz}{y^2}+\dfrac{xy}{z^2}=3\)
Cho các số thực x,y,z khác 0, đôi một khác nhau và thỏa điều kiện
\(x^2-xy=y^2-yz=z^2-zx=a\left(a\inℝ\right)\)
a) Chứng minh rằng \(a\ne0\), từ đó suy ra \(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=0\)
b) Chứng minh rằng \(\frac{x}{z}+\frac{z}{y}+\frac{y}{x}=-3\)
Cho a,b,c là các hằng số và a khác -1, b khác -1, c khác -1. Chứng minh rằng nếu x=b*y+c*z; y=a*x+c*z; z=a*x+b*y; x+y+z khác 0 thì 1/(1+a)+1/(1+b)+1/(1+c)=2
3 tháng 8 2023 lúc 16:33
Cho x, y, z là 3 số khác 0 thoả mãn x + y + z 0. Chứng minh rằng:
sqrt{dfrac{1}{x^2}+dfrac{1}{y^2}+dfrac{1}{z^2}}left|dfrac{1}{x}+dfrac{1}{y}+dfrac{1}{z}right|
Đọc tiếp
Cho \(x\), \(y\), \(z\) là 3 số khác 0 thoả mãn \(x\) \(+\) \(y\) \(+\) \(z\) \(=0\). Chứng minh rằng:
\(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}\)=\(\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)
cho x,y thuộc Q,x khác 0, y khác 0 thỏa mãn \(x^3+y^3=2x^2y^2\).Chứng minh rằng A=\(\sqrt{1-\frac{1}{xy}}\)là một số hữu tỉ
giải giúp mình với
A=\(\dfrac{\sqrt{x}+1}{\sqrt{x}-2}\) và \(B=\dfrac{\sqrt{x}-2}{\sqrt{x}}\) đk : x> 0; x khác 4
Cho P = A.B
Tìm GTNN của P
Cho P = \(\dfrac{\sqrt{x}+2}{2\sqrt{x}+1}\) (đk x>-0 ; x khác 1/2 )
TÌM X BT |P| > HOẶC BẰNG P