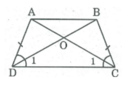
Câu 1:Cho hình thang ABCD(AB//CD). Gọi O là giao điểm của 2 đường chéo
a, Chứng minh rằng \(\frac{OA}{OC}=\frac{OB}{OD}\)
b, Đường thẳng qua O cắt AB tại M, CD tại N. Chứng minh rằng \(\frac{OM}{AB}=\frac{ON}{CD}\)
Câu 2:Cho ΔABC vuông tại A đường cao AH. Tia phân giác \(\widehat{ABC}\) cắt AH và AC lần lượt tại E và F.
a, Chứng minh ΔABC ∼ ΔHBA. Từ đó suy ra \(AB^2\)=BH.BC
b, Chứng minh \(\frac{EH}{AE}=\frac{FA}{FC}\)