Một hình nón có diện tích xung quanh 80π cm², diện tích đáy bằng 36π cm². Tính thể tích hình nón.

Những câu hỏi liên quan
Cho một hình nón có bán kính đáy là r= 4 cm, diện tích đáy bằng 4/5 diện tích xung quanh của nó. Tính thể tích hình nón đã cho.
Cho hình nón có bán kính đáy R=3 cm, biết diện tích xung quanh bằng hai lần diện tích đáy của nó. Tính thể tích hình nón.
Lời giải:
Theo bài ra ta có:
$\pi rl=2\pi r^2$
$\Rightarrow l=2r=6$ (cm)
Mà theo định lý Pitago: $l^2=h^2+r^2$
$\Rightarrow h=\sqrt{l^2-r^2}=3\sqrt{3}$ (cm)
Thể tích hình nón:
$V=\frac{1}{3}\pi r^2h=\frac{1}{3}.\pi. 3^2.3\sqrt{3}=9\sqrt{3}\pi$ (cm3)
Đúng 0
Bình luận (0)
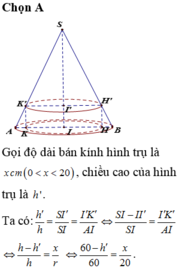
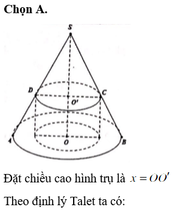
Cho hình nón (N) có bán kính đáy r20(cm), chiều cao h60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
Đọc tiếp
Cho hình nón (N) có bán kính đáy r=20(cm), chiều cao h=60(cm) và một hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
![]()
![]()
![]()
![]()
Cho hình nón (N) có bán kính r 20(cm), chiều cao h 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất? A. V3000
π
(
cm
3
)
. B. V
32000
9...
Đọc tiếp
Cho hình nón (N) có bán kính r = 20(cm), chiều cao h = 60(cm) và mọt hình trụ (T) nội tiếp hình nón (N) (hình trụ (T) có một đáy thuộc đáy hình nón và một đáy nằm trên mặt xung quanh của hình nón). Tính thể tích V của hình trụ (T) có diện tích xung quanh lớn nhất?
A. V=3000 π ( cm 3 ) .
B. V= 32000 9 π ( cm 3 ) .
C. V=3600 π ( cm 3 ) .
D. V=4000 π ( cm 3 ) .
Một hình nón có độ dài đường sinh là 16cm và có diện tích xung quanh là 80π ( c m 2 ). Bán kính đáy của hình nón bằng:
A.3cm
B.4 cm
C.5 cm
D.6 cm
Một hình nón có đường cao bằng 10 cm, bán kính đáy r 15 cm. Tính diện tích xung quanh của hình nón đó A.
75
13
B.
5
π
13
C.
125
π
13
D.
75...
Đọc tiếp
Một hình nón có đường cao bằng 10 cm, bán kính đáy r = 15 cm. Tính diện tích xung quanh của hình nón đó
A. 75 13
B. 5 π 13
C. 125 π 13
D. 75 π 13
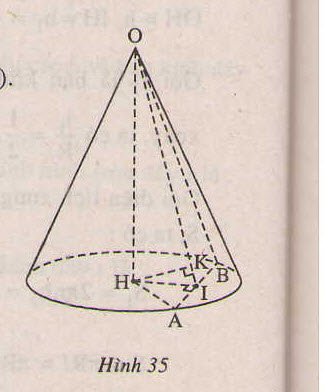
Cho hình nón tròn xoay có đường cao h = 20 cm, bán kính đáy r = 25 cm.
a) Tính diện tích xung quanh của hình nón đã cho.
b) TÍnh thể tích của khối nón được tạo bởi hình nón đó.
c) Một thiết diện đi qua đỉnh của hình nón có khoảng cách từ tâm của đáy đến mặt phẳng chứa thiết diện là 12 cm. Tính diện tích thiết diện đó.
a) Đường sinh l của hình nón là:
l = =
= 5√41 (cm).
Diện tích xung quanh của hình nón là:
Sxq = πrl = 125π√41 (cm2)
b) Vnón = = (625.20π)/3 = (12500π)/3 (cm3)
c) Giả sử thiết diện cắt hình tròn đáy theo đoạn thẳng AB.
GỌi I là trung điểm AB, O là đỉnh của nón thì thiết diện là tam giác cân OAB.
Hạ HK vuông góc AI, H là tâm của đáy, thì HK vuông góc ( OAB) và theo giả thiết HK = 12 (cm)
Đúng 0
Bình luận (0)
Một hình nón có đường cao bằng 10 cm, bán kính đáy r= 15cm. Tính diện tích xung quanh của hình nón đó.
A.75 13
B. 5 π 13
C.125 π 13
D.75 π 13
Đáp án: D
Diện tích xung quanh:
![]()
Ta xét tam giác vuông SOA:
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho hình nón có đường kính đáy d 10 cm và diện tích xung quanh 65π (cm2) . Tính thể tích khối nón: A. 100
π
(
c
m
3
) B. 120
π
(
c
m
3
) C. 300
π
(
c
m
3
) D. 200
π
(
c
m
3
)
Đọc tiếp
Cho hình nón có đường kính đáy d = 10 cm và diện tích xung quanh 65π (cm2) . Tính thể tích khối nón:
A. 100 π ( c m 3 )
B. 120 π ( c m 3 )
C. 300 π ( c m 3 )
D. 200 π ( c m 3 )