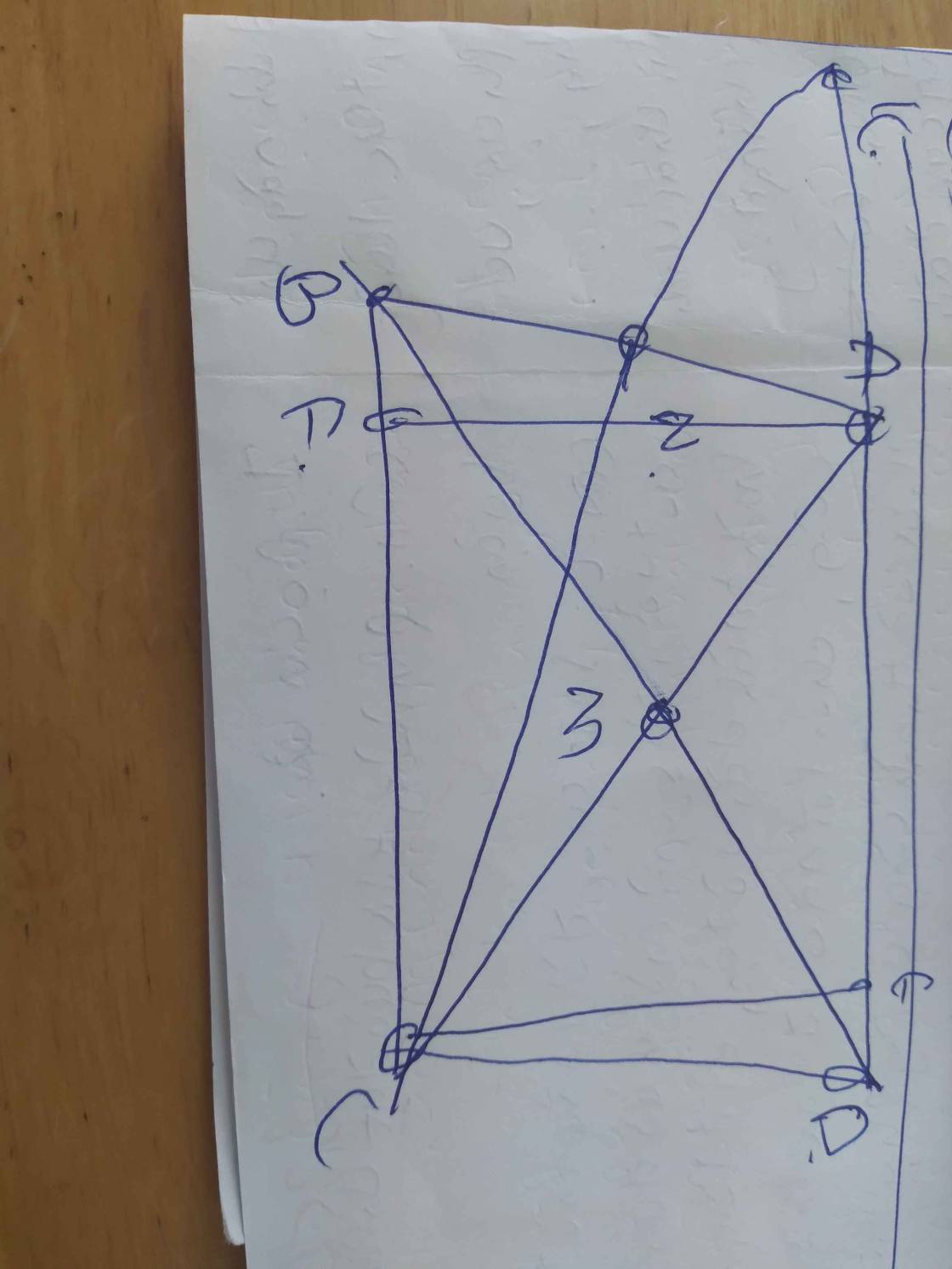
- Cho tam giác ABC . Trên tia đối của tia CB lấy điểm M sao cho CM=CB. Trên tia đối của tia CA lấy điểm D sao cho CD=CA
a) Chứng minh tam giác ABC= tam giác CMD
b) Chứng minh MD//AB
c) Gọi I là trung điể, nằm giữa A và B . Tia CI cắt Md tại điểm N. So sánh độ dài các đoạn thẳng BI và NM,IA và ND