Tính giá trị nhỏ nhất của biểu thức A (x>0)
A=x3-3x2+4+2016x
Bài 1: Tìm giá trị nhỏ nhất của biểu thức [(x+1/2)2 + 5/4]
Bài 2: Cho đa thức M= x3+x2y-3x2-xy-y2+4y+x+2019
Tính giá trị của đa thức M biết x+y-3=0
Bài 1:
Ta thấy: $(x+\frac{1}{2})^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow (x+\frac{1}{2})^2+\frac{5}{4}\geq \frac{5}{4}$
Vậy gtnn của biểu thức là $\frac{5}{4}$
Giá trị này đạt tại $x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}$
Bài 2:
$x+y-3=0\Rightarrow x+y=3$
\(M=x^2(x+y)-(x+y)x^2-y(x+y)+4y+x+2019\)
\(=-3y+4y+x+2019=x+y+2019=3+2019=2022\)
Cho hai số thực x, y thỏa mãn x ≥ 0 , y ≥ 1 , x + y = 3. Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 3 + 2 y 2 + 3 x 2 + 4 xy − 5 x .
A. P max = 15 v à P min = 13.
B. P max = 20 v à P min = 18
C. P max = 20 v à P min = 15.
D. P max = 18 v à P min = 15.
Cho hai số thực x,y thỏa mãn x ≥ 0 , y ≥ 1 , x + y = 3 . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 3 + 2 y 2 + 3 x 2 + 4 x y - 5 x .
A. P max = 15 và P min = 13 .
B. P max = 20 và P min = 18
C. P max = 20 và P min = 15
D. P max = 18 và P min = 18
Cho hai số thực x, y thỏa mãn x≥ 0; y≥1 ; x+ y= 3 . Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P= x3+ 2y2+ 3x2+ 4xy- 5x lần lượt bằng:
A. 20 và 18 .
B. 20 và 15.
C. 16 và 15 .
D. 16 và 13.
Ta có y= 3-x≥ 1 nên x≤ 2 do đó : x
Khi đó P= x3+ 2( 3-x) 2+ 3x2+4x( 3-x) -5x= x3+x2-5x+18
Xét hàm số f(x) = x3+x2-5x+18 trên đoạn [0 ; 2] ta có:
f ' ( x ) = 3 x 2 + 2 x - 5 ⇒ f ' ( x ) = 0 x ∈ ( 0 ; 2 ) ⇔
F(0) =18; f(1) = 15; f(2) =20
Vậy giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P lần lượt bằng 20 và 15.
Chọn B.
Cho hai số thực x, y thỏa mãn x ≥ 0 , y ≥ 1 , x + y = 3. Giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 3 + 2 y 2 + 3 x 2 + 4 x y − 5 x lần lượt bằng
A. P m a x = 15 v à P min = 13
B. P m a x = 20 v à P min = 18
C. P m a x = 20 v à P min = 15
D. P m a x = 18 v à P min = 15
Đáp án C
Ta có x + y = 3 ⇒ y = 3 − x ≥ 1 ⇔ x ≤ 2 ⇒ x ∈ 0 ; 2
Khi đó P = f x = x 3 + 2 3 − x 2 + 3 x 2 + 4 x 3 − x − 5 x = x 3 + x 2 − 5 x + 18
Xét hàm số f x = x 3 + x 2 − 5 x + 18 trên đoạn 0 ; 2 , có f ' x = 3 x 2 + 2 x − 5
Phương trình 0 ≤ x ≤ 2 3 x 2 + 2 x − 5 = 0 ⇔ x = 1. Tính f 0 = 18 , f 1 = 15 , f 2 = 20
Vậy min 0 ; 2 f x = 15 , m a x 0 ; 2 f x = 20 hay P m a x = 20 và P min = 15
Cho biểu thức A = x 3 – 3 x 2 + 3 x . Tính giá trị của A khi x = 1001
A. A = 1000 3
B. A = 1001
C. A = 1000 3 - 1
D. A = 1000 3 + 1
Ta có
A = x 3 – 3 x 2 + 3 x = x 3 – 3 x 2 + 3 x – 1 + 1 = ( x – 1 ) 3 + 1
Thay x = 1001 vào A = ( x – 1 ) 3 + 1 ta được
A = ( 1001 – 1 ) 3 + 1 suy ra A = 10003 + 1
Đáp án cần chọn là: D
Tính giá trị của biểu thức sau tại x = 3, x = -1
a. A = 3x2 - 1
b.B= x3 - 2x
a: A(3)=3*3^2-1=27-1=26
A(-1)=3-1=2
b: B(3)=3^3-2*3=27-6=21
B(-1)=(-1)^3-2*(-1)=-1+2=1
Tính giá trị lớn nhất và nhỏ nhất của hàm số:
y = x 3 - 3 x 2 - 9 x + 35 trên các đoạn [-4; 4] và [0; 5
TXĐ: D = R.
y ' = 3 x 2 - 6 x - 9 ;
y' = 0 ⇔ x = –1 hoặc x = 3.
+ Xét hàm số trên đoạn [-4; 4] :
y(-4) = -41 ;
y(-1) = 40 ;
y(3) = 8
y(4) = 15.
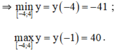
+ Xét hàm số trên [0 ; 5].
y(0) = 35 ;
y(3) = 8 ;
y(5) = 40.
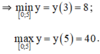
Tìm giá trị nhỏ nhất của biểu thức: A=\(\frac{2016x+3780}{x^2+1}\)