Cho ba số bất kì a, a, c .Chứng tỏ rằng a2 + b2 + c2 ≥ a ( b+c). Dấu = xảy ra khi nào

Những câu hỏi liên quan
Bài 3 : (3đ)
1. Chứng minh rằng với hai số thực bất kì a,b ta luôn có : left(dfrac{a+b}{2}right)^2ge ab
Dấu bằng xảy ra khi nào ?
2. Cho ba số thực a,b,c không âm sao cho a+b+c1
Chứng minh : b+cge16abc . Dấu bằng xảy ra khi nào ?
Nhân tiện em cũng hỏi luôn là tại sao khi em đăng bài mặc dù em đã điền đủ lớp môn ; mạng không lag mà sao vẫn không thể đăng bài được . Em phải mất tận 2 lần ghi lại đề bài mới có thể đăng bài được.
Đọc tiếp
Bài 3 : (3đ)
1. Chứng minh rằng với hai số thực bất kì a,b ta luôn có : \(\left(\dfrac{a+b}{2}\right)^2\ge ab\)
Dấu bằng xảy ra khi nào ?
2. Cho ba số thực a,b,c không âm sao cho \(a+b+c=1\)
Chứng minh : \(b+c\ge16abc\) . Dấu bằng xảy ra khi nào ?
Nhân tiện em cũng hỏi luôn là tại sao khi em đăng bài mặc dù em đã điền đủ lớp môn ; mạng không lag mà sao vẫn không thể đăng bài được . Em phải mất tận 2 lần ghi lại đề bài mới có thể đăng bài được.
3.1
Xét hiệu :
\(\left(\dfrac{a+b}{2}\right)^2-ab=\dfrac{a^2+2ab+b^2}{4}-\dfrac{4ab}{4}\)
\(=\dfrac{a^2-2ab+b^2}{4}=\dfrac{\left(a-b\right)^2}{4}\ge0\forall a,b\in R\)
Vậy \(\left(\dfrac{a+b}{2}\right)^2\ge ab,\forall a,b\in R\)
Dấu bằng xảy ra : \(\Leftrightarrow a=b\)
3.2
Áp dụng kết quả của câu 3.1 vào câu 3.2 ta được:
\(\left(a+b+c\right)^2=[a+\left(b+c\right)]^2\ge4a\left(b+c\right)\)
Mà : \(a+b+c=1\left(gt\right)\)
nên : \(1\ge4a\left(b+c\right)\)
\(\Leftrightarrow b+c\ge4a\left(b+c\right)^2\) ( vì a,b,c không âm nên b+c không âm )
Mà : \(\left(b+c\right)^2\ge4bc\Leftrightarrow\left(b-c\right)^2\ge0,\forall b,c\in N\)
\(\Rightarrow b+c\ge16abc\)
Dấu bằng xảy ra : \(\Leftrightarrow\left\{{}\begin{matrix}a=b+c\\b=c\end{matrix}\right.\Leftrightarrow b=c=\dfrac{1}{4};a=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
Cho a,b,c thuộc R . CM Bất đẳng thức sau và cho biết dấu = xảy ra khi nào?
g) a2+b2+c2-4a-6b-2c+14 ≥0
h) a 2+4b2+3c2 +14> 2a+12b+6c
Mn làm giúp dùm e bài này với ạ.
a: \(\Leftrightarrow a^2-4a+4+b^2-6b+9+c^2-2c+1>=0\)
\(\Leftrightarrow\left(a-2\right)^2+\left(b-3\right)^2+\left(c-1\right)^2>=0\)
Dấu '=' xảy ra (a,b,c)=(2;3;1)
Đúng 1
Bình luận (1)
Cho a,b,c∈Ra,b,c∈R và a2+b2+c2=21a2+b2+c2=21. Chứng minh rằng: 7≤|a−2b|+|b−2c|+|c−2a|≤√3997≤|a−2b|+|b−2c|+|c−2a|≤399 Ý tưởng: ( Nhưng không chắc chắn là đúng hướng :'> ) Dùng bất đẳng thức Cauchy-Schwarz để chứng minh bài toán -> x1+x2+...+xn≤|x1|+|x2|+...+|xn|≤√n(x21+x22+...+x2n)
Trong tam giác ABC. Chứng minh rằng
a) Góc A nhọn khi và chỉ khi a2 < b2 + c2
b) Góc A tù khi và chỉ khi a2 > b2 + c2
c) Góc A vuông khi và chỉ khi a2 = b2 + c2
Trong tam giác ABC, theo Hệ quả định lý Cô sin ta luôn có :
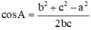
Mà ta có 2.bc > 0 nên cos A luôn cùng dấu với b2 + c2 – a2.
a) Góc A nhọn ⇔ cos A > 0 ⇔ b2 + c2 – a2 > 0 ⇔ a2 < b2 + c2.
b) Góc A tù ⇔ cos A < 0 ⇔ b2 + c2 – a2 < 0 ⇔ a2 > b2 + c2.
c) Góc A vuông ⇔ cos A = 0 ⇔ b2 + c2 – a2 = 0 ⇔ a2 = b2 + c2.
Đúng 0
Bình luận (0)
với a b c là 3 số bất kì cm a2+b2+c2+3≥2(a+b+c)
Ta có:
\(\left(a-1\right)^2\ge0;\forall a\) (1)
\(\left(b-1\right)^2\ge0;\forall b\) (2)
\(\left(c-1\right)^2\ge0;\forall c\) (3)
Cộng từng vế (1);(2);(3) ta được:
\(\left(a-1\right)^2+\left(b-1\right)^2+\left(c-1\right)^2\ge0\)
\(\Leftrightarrow a^2-2a+1+b^2-2b+1+c^2-2c+1\ge0\)
\(\Leftrightarrow a^2+b^2+c^2-2\left(a+b+c\right)+3\ge0\)
\(\Leftrightarrow a^2+b^2+c^2+3\ge2\left(a+b+c\right)\) ( đfcm )
Đúng 1
Bình luận (0)
Ta có:
(a−1)2≥0;∀a(a−1)2≥0;∀a (1)
(b−1)2≥0;∀b(b−1)2≥0;∀b (2)
(c−1)2≥0;∀c(c−1)2≥0;∀c (3)
Cộng từng vế (1);(2);(3) ta được:
(a−1)2+(b−1)2+(c−1)2≥0(a−1)2+(b−1)2+(c−1)2≥0
⇔a2−2a+1+b2−2b+1+c2−2c+1≥0⇔a2−2a+1+b2−2b+1+c2−2c+1≥0
⇔a2+b2+c2−2(a+b+c)+3≥0⇔a2+b2+c2−2(a+b+c)+3≥0
⇔a2+b2+c2+3≥2(a+b+c)⇔a2+b2+c2+3≥2(a+b+c) ( đpcm ).
Đúng 0
Bình luận (0)
Giả sử `a^2+b^2+c^2+3ge2.(a+b+c)`
`<=>a^2+b^2+c^2+3ge2a+2b+2c`
`<=>a^2+b^2+c^2+3-2a-2b-2cge0`
`<=>(a^2-2a+1)+(b^2-2b+1)+(c^2-2c+1)ge0`
`<=>(a-1)^2+(b-1)^2+(c-1)^2ge0(text{luôn đúng})`
Dấu `=` xảy ra khi:`a=b=c=1`
Đúng 1
Bình luận (0)
Cho a, b, c là độ dài ba cạnh của tam giác. Sử dụng định lí về dấu tam thức bậc hai, chứng mình rằng:
b2x2 - (b2 + c2 - a2)x + c2 > 0 ∀x
Xét tam thức f(x) = b2x2 - (b2 + c2 - a2)x + c2 có:
Δ = (b2 + c2 - a2)2 - 4b2c2
= (b2 + c2 - a2 - 2bc)(b2 + c2 - a2 + 2bc)
= [(b - c)2 - a2][(b + c)2 - a2]
= (b – c – a)(b – c + a)(b + c + a)(b + c – a).
Do a, b, c là 3 cạnh của tam giác nên theo bất đẳng thức tam giác ta có:
b < c + a ⇒ b – c – a < 0
c < a + b ⇒ b – c + a > 0
a < b + c ⇒ b + c – a > 0
a, b, c > 0 ⇒ a + b + c > 0
⇒ Δ < 0 ⇒ f(x) cùng dấu với b2 ∀x hay f(x) > 0 ∀x (đpcm).
Đúng 0
Bình luận (0)
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 - 2 a b ≥ 0
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
Đúng 0
Bình luận (0)
Chứng tỏ rằng với a và b là các số bất kì thì: a 2 + b 2 / 2 ≥ a b
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b
⇒ a 2 + b 2 . 1 / 2 ≥ 2 a b . 1 / 2 ⇒ a 2 + b 2 / 2 ≥ a b
Đúng 0
Bình luận (0)
Câu 29. Chứng minh các bất đẳng thức:a) (a + b)2 ≤ 2(a2 + b2)b) (a + b + c)2 ≤ 3(a2 + b2 + c2)c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).Câu 30. Cho a3 + b3 2. Chứng minh rằng a + b ≤ 2.Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].Câu 32. Tìm giá trị lớn nhất của biểu thức: Câu 33. Tìm giá trị nhỏ nhất của: với x, y, z 0.Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:a) ab và a/b là số vô tỉ.b) a + b và a/b là số hữu tỉ (a + b ≠ 0)c) a + b, a2 và b2 là số hữu tỉ (a + b ≠...
Đọc tiếp
Câu 29. Chứng minh các bất đẳng thức:
a) (a + b)2 ≤ 2(a2 + b2)
b) (a + b + c)2 ≤ 3(a2 + b2 + c2)
c) (a1 + a2 + ….. + an)2 ≤ n(a12 + a22 + ….. + an2).
Câu 30. Cho a3 + b3 = 2. Chứng minh rằng a + b ≤ 2.
Câu 31. Chứng minh rằng: [x] + [y] ≤ [x + y].
Câu 32. Tìm giá trị lớn nhất của biểu thức: ![]()
Câu 33. Tìm giá trị nhỏ nhất của: ![]() với x, y, z > 0.
với x, y, z > 0.
Câu 36. Xét xem các số a và b có thể là số vô tỉ không nếu:
a) ab và a/b là số vô tỉ.
b) a + b và a/b là số hữu tỉ (a + b ≠ 0)
c) a + b, a2 và b2 là số hữu tỉ (a + b ≠ 0)
Câu 37. Cho a, b, c > 0. Chứng minh: a3 + b3 + abc ≥ ab(a + b + c)
Câu 38. Cho a, b, c, d > 0. Chứng minh:
![]()
Câu 39. Chứng minh rằng [2x] bằng 2[x] hoặc 2[x] + 1
Câu 40. Cho số nguyên dương a. Xét các số có dạng: a + 15 ; a + 30 ; a + 45 ; … ; a + 15n. Chứng minh rằng trong các số đó, tồn tại hai số mà hai chữ số đầu tiên là 96.
Câu 41. Tìm các giá trị của x để các biểu thức sau có nghĩa:
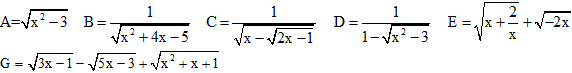 Mn giúp em với ;-;
Mn giúp em với ;-;
















