Với giá trị nào của x thì \(\frac{x-1}{x+1}\)>0

Những câu hỏi liên quan
Cho biểu thức: \(P=\left(\frac{1}{\sqrt{x}-1}-\frac{1}{\sqrt{x}}\right):\left(\frac{\sqrt{x}+1}{\sqrt{x}-2}-\frac{\sqrt{x}+2}{\sqrt{x}-1}\right)\) Với x>0;x#1;x#4
a,Rút gọn P
b,Với giá trị nào của x thì P=\(\frac{1}{4}\)
c,Tính giá trị của P tại x=\(4+2\sqrt{3}\)
a: \(P=\dfrac{\sqrt{x}-\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-2\right)\left(\sqrt{x}-1\right)}{x-1-x+4}\)
\(=\dfrac{1}{\sqrt{x}}\cdot\dfrac{\sqrt{x}-2}{3}=\dfrac{\sqrt{x}-2}{3\sqrt{x}}\)
b: P=1/4
=>\(\dfrac{\sqrt{x}-2}{3\sqrt{x}}=\dfrac{1}{4}\)
=>\(4\left(\sqrt{x}-2\right)=3\sqrt{x}\)
=>\(4\sqrt{x}-8-3\sqrt{x}=0\)
=>\(\sqrt{x}=8\)
=>x=64
c: Khi \(x=4+2\sqrt{3}\) thì \(P=\dfrac{\sqrt{4+2\sqrt{3}}-2}{3\cdot\sqrt{4+2\sqrt{3}}}\)
\(=\dfrac{\sqrt{3}+1-2}{3\left(\sqrt{3}+1\right)}=\dfrac{\sqrt{3}-1}{3\sqrt{3}+3}=\dfrac{2-\sqrt{3}}{3}\)
Đúng 1
Bình luận (0)
Cho biểu thức:
\(A=\left(\frac{x^2}{x^3-4x} +\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
a) Rút gọn A
b) Tìm giá trị của biểu thức khi /x/=\(\frac{1}{2}\)
c) Với giá trị nào của x thì A=2
d) Với giá trị nào của x thì A<0
e) Tìm giá trị nguyên của x để A nhận giá trị nguyên
với giá trị nào của biến thì giá trị của biểu thức sau bằng 0
\(\frac{x+1}{7};\frac{3x+3}{5};\frac{3x\left(x-5\right)}{x-7};\frac{2x\left(x+1\right)}{3x+4}\)
Cho \(C=\left(\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{\sqrt{x}+2}{3-\sqrt{x}}+\frac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right):\left(1-\frac{\sqrt{x}}{\sqrt{x}+1}\right)\)
a) Rút gọn C
b)Tìm giá trị nguyên của x để C<0
c)với giá trị nào của x thì 1/C đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
a) Với giá trị nào của x thì x^2-2x<0
b) Với giá trị nào của x thì
(x-1).(-x+2)> hoặc = 0
lập bảng xét dấu đi bạn. a. 0<x<2
b. 1<=x<=2
Đúng 0
Bình luận (0)
Lập bảng xét dấu ta đc \(\Rightarrow0< x< 2\)
b)\(\left(x-1\right)\left(-x+2\right)\ge0\)
\(\Leftrightarrow\begin{cases}x-1\ge0\\-x+2\ge0\end{cases}\) hoặc \(\begin{cases}x-1\le0\\-x+2\le0\end{cases}\)
\(\Leftrightarrow\begin{cases}x\ge1\\x\le2\end{cases}\) hoặc \(\begin{cases}x\le1\\x\ge2\end{cases}\)
\(\Rightarrow1\le x\le2\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
cho biểu thứcP=\(\frac{\sqrt{x}-2}{\sqrt{x}+1}\)
a)tìm các giá trị của x để P<0
b)với giá trị nào của x thì P đạt giá trị nhỏ nhất.tìm giá trị ấy
a, \(P=\frac{\sqrt{x}-2}{\sqrt{x}+1}< 0\)
\(\Rightarrow\sqrt{x}-2< 0\)( vì \(\sqrt{x}+1>0\))
\(\Rightarrow\sqrt{x}>2\Rightarrow x>4\)
Vậy với P < 0 thì x > 4
b, \(P=\frac{\sqrt{x}-2}{\sqrt{x}+1}=\frac{\sqrt{x}+1-3}{\sqrt{x}+1}=1-\frac{3}{\sqrt{x}+1}\ge1\)
Dấu bằng xảy ra khi \(\sqrt{x}+1>0\)
1.Cho phương trình:\(\left(m+1\right)x^2-2\left(m+1\right)+m-3=0\)0
a)Với giá trị nào của m thì pt có nghiệm kép.Tính nghiệm kép
b)Với giá trị nào của m thì pt có nghiệm:\(x_1x_2\)
2.\(A=\frac{x}{x-4}+\frac{1}{\sqrt{x}-2}+\frac{1}{\sqrt{x+2}}\)
a)Rút gọn A
b)Tính x khi \(A=-\frac{1}{3}\)
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
Với giá trị nào của x thì giá trị của mỗi biểu thức sau bằng 0: 1 x 2 + x + 1 + x - 1
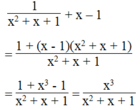
Biểu thức bằng 0 khi x 3 = 0 và x 2 + x + 1 ≠ 0
Ta có: x 3 = 0 ⇒ x = 0;
x 2 + x + 1 = x 2 + 2 . x . 1 / 2 + 1 / 4 + 3 / 4 = x + 1 / 2 2 + 3 / 4 ≠ 0 mọi x.
Vậy với x = 0 thì giá trị của biểu thức bằng 0.
Đúng 0
Bình luận (0)
với giá trị nào của x thì giá trị phân thức sau:
\(A=\frac{-2}{x+1}>0\)
\(B=\frac{-3}{x+2}0\)


















