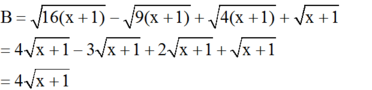rút gọn biểu thức dưới đây : A= (3x+4) (9x^2- 12x +16) - ( 16+ 27x^30)

Những câu hỏi liên quan
Rút gọn biểu thức sau:
a)M=\(3x-\sqrt[3]{27^3+27x^2+9x+1}\)
b)N=\(\sqrt[3]{8x^3+12x^2+6x+1}-\sqrt[3]{x^3}\)
a: Sửa đề: \(M=3x-\sqrt[3]{27x^3+27x^2+9x+1}\)
\(=3x-\sqrt[3]{\left(3x\right)^3+3\cdot\left(3x\right)^2\cdot1+3\cdot3x\cdot1^2+1^3}\)
\(=3x-\sqrt[3]{\left(3x+1\right)^3}\)
\(=3x-3x-1=-1\)
b: \(N=\sqrt[3]{8x^3+12x^2+6x+1}-\sqrt[3]{x^3}\)
\(=\sqrt[3]{\left(2x\right)^3+3\cdot\left(2x\right)^2\cdot1+3\cdot2x\cdot1^2+1^3}-x\)
\(=\sqrt[3]{\left(2x+1\right)^3}-x\)
=2x+1-x
=x+1
Đúng 0
Bình luận (0)
bài 1
a) rút gọn biểu thức : A= 4√12+ 3√75 -5√48
b) giải phương trình :√x-2 -√9x-18 =16
a ⇒A=\(4\sqrt{4\times3}+3\sqrt{25\times3}-5\sqrt{16\times3}=8\sqrt{3}+15\sqrt{3}-20\sqrt{3}=3\sqrt{3}\)
b ĐKXĐ x≥2 ⇔\(\sqrt{x-2}+3\sqrt{x-2}=16\Leftrightarrow4\sqrt{x-2}=16\Leftrightarrow\sqrt{x-2}=4\Rightarrow x-2=16\Leftrightarrow x=18\)
Đúng 0
Bình luận (0)
a. \(A=4\sqrt{12}+3\sqrt{75}-5\sqrt{48}\)
\(=8\sqrt{3}+15\sqrt{3}-20\sqrt{3}\)
\(=3\sqrt{3}\)
b. \(\sqrt{x-2}-\sqrt{9x-18}=16\)
\(\Leftrightarrow\sqrt{x-2}-\sqrt{9\left(x-2\right)}=16\)
\(\Leftrightarrow\sqrt{x-2}-3\sqrt{x-2}=16\)
\(\Leftrightarrow-2\sqrt{x-2}=16\)
\(\Leftrightarrow\sqrt{x-2}=-8\) ( Vô lý )
Vậy PT vô nghiệm
Đúng 0
Bình luận (0)
a, 4\(\sqrt{12}+3\sqrt{75}-5\sqrt{48}\)
=\(8\sqrt{3}+15\sqrt{3}-20\sqrt{3}\)
= (8+15-20)\(\sqrt{3}\) = 3\(\sqrt{3}\)
Đúng 0
Bình luận (0)
Bài: giải các phương trình sau:
a/2x(27x^2-8)+4(2x-6)(2x+6)-(3x-4)(5x+2)=2(3x-4)(9x^2+12x+16).
b/ 4-x/2018-2=3-x/2019-x/1011
Thu gọn đa thức
M=(3x - 4)(9x2 - 12x + 16) +(6x - 8)2
\(M=\left(3x-4\right)\left(9x^2-12x+16\right)+\left(6x+8\right)^2\)
\(\Rightarrow M=\left(3x-4\right)\left(3x-4\right)^2+4\left(3x-4\right)^2\)
\(\Rightarrow M=\left(3x-4\right)^2\left(3x-4+4\right)\)
\(\Rightarrow M=\left(3x-4\right)^2.3x\)
Đúng 0
Bình luận (0)
Ko ghi lại đề
\(=>M=\left(3X-4\right)\left(3x-4\right)^2+4\left(3x-4\right)^2\)
\(=>M=\left(3X-4\right)^2\left(3x-4+4\right)\)
\(=>M=\left(3X-4\right)^2\left(3x\right)\)
~Study well~ :)
Đúng 0
Bình luận (0)
Cho biểu thức
B = 16 x + 16 − 9 x + 9 + 4 x + 4 + x + 1
với x ≥ -1.
a) Rút gọn biểu thức B;
b) Tìm x sao cho B có giá trị là 16.
a) Rút gọn:
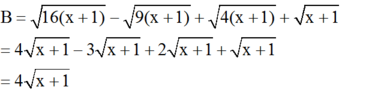
b) Để B = 16 thì:
![]()
⇔ x + 1 = 16 ⇔ x = 15 (thỏa mãn x ≥ -1)
Đúng 0
Bình luận (0)
Viết các biểu thức sau dưới dạng bình phương một tổng hc một hiệu
a)x^3+9x^2+27x+27
b)8-12x+6x^2-x^3
c)x^6-3x^5+3x^4-x^3
a, x^3 +3.3.x^2+3.3^2.x+3^3
= (x+3)^3.
b , 23-3*x*22+3*x2*2-x3
<=> (2-x)3
c, (x2)3-3*(x2)2*x+3*x2*x2-x3
<=> (x2-x)3
Đúng 0
Bình luận (0)
rút gọn các biểu thức:
a) \(A=\sqrt{x^2+8x+16}+\sqrt{x^2-8x+16}Với\)VỚI \(-4\le x\le4\)
b) \(B=\sqrt{9x^2-6x+1}+\sqrt{4x^2-12x+9}\)
AI LM ĐÚNG MK TIK CHO NHÉ, CAMON TRC
a, Với \(-4\le x\le4\)
\(A=\sqrt{x^2+8x+16}+\sqrt{x^2-8x+16}\)
\(=\sqrt{\left(x+4\right)^2}+\sqrt{\left(x-4\right)^2}=\left|x+4\right|+\left|x-4\right|\)
b, \(B=\sqrt{9x^2-6x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(3x\right)^2-2.3x+1}+\sqrt{\left(2x\right)^2-2.2x.3x+3^2}\)
\(=\sqrt{\left(3x-1\right)^2}+\sqrt{\left(2x-3\right)^2}=\left|3x-1\right|+\left|2x-3\right|\)
Cho biểu thức B = 16 x + 16 - 9 x + 9 + 4 x + 4 + x + 1
với x ≥ -1.
Rút gọn biểu thức B;
Cho biểu thức B= \(\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\) với \(x\ge-1\).
a) Rút gọn biểu thức B.
b) tìm x sao cho B có giá trị là 16.
a.
\(B=\sqrt{16x+16}-\sqrt{9x+9}+\sqrt{4x+4}+\sqrt{x+1}\left(x\ge-1\right)\)
\(B=\sqrt{16}.\sqrt{x+1}-\sqrt{9}.\sqrt{x+1}+\sqrt{4}.\sqrt{x+1}+\sqrt{x+1}\)
\(B=4\sqrt{x+1}-3\sqrt{x+1}+2\sqrt{x+1}+\sqrt{x+1}\)
\(B=\left(4-3+2+1\right).\sqrt{x+1}\)
\(B=4.\sqrt{x+1}\)
b.
\(B=16\\\)
\(\Rightarrow4\sqrt{x+1}=16\)
\(\Rightarrow\sqrt{x+1}=\dfrac{16}{4}=4\)
\(\Rightarrow x+1=4^2\)
\(\Rightarrow x+1=16\rightarrow x=16-1=15\) (thỏa mãn)
vậy x=15
Đúng 2
Bình luận (0)