Bài 1 Cho 3 điểm A,F,B thẳng hàng (F nằm giữa A và B).Vẽ đường tròn tâm O đường kính AF; vẽ đường tròn O' đường kính AB.Dây cung BE của đường tròn O' t/x với đường tròn O tại C. Đoạn AC kéo dài cắt O' tại D.CM rằng:
a,AE song song OC
b,AD là pg của BAE
c,tam giác ABC đồng dạng với tam giác CBF
d, AC.AD + BC.BE= AB bình phương
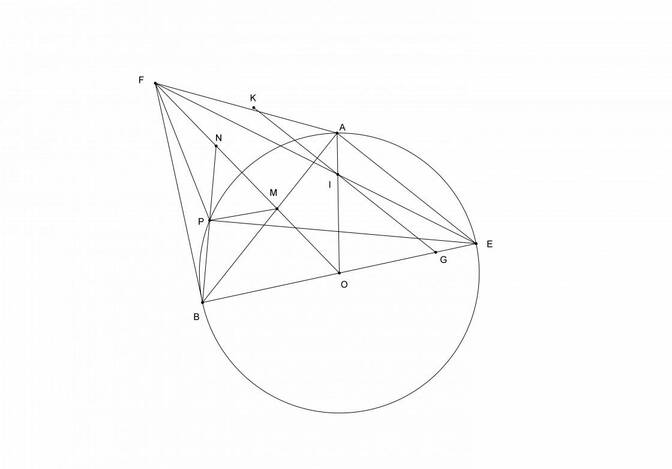
Bài 2 Cho tam giác ABC (AC>AB; góc BAC>90).Gọi I,K theo thứ tự là các trung điểm của AB AC.Các đường tròn đường kính AB,AC cắt nhau tại điểm thứ hai D;tia BA cắt đường tròn K tại điểm thứ hai E;tia CA cắt đường tròn I tại điểm thứ hai F.
a,B,C,D thằng hàng
b,Tứ giác BFEC nội tiếp
c, AD BF CE đồng quy
d,Gọi H là giao điểm thứ hai của tia DF với đường tròn ngoại tiếp tam giác AEF.Hãy so sánh DH DE
Bài 3: Cho đường tròn( O;R) và điểm A nằm ở ngoài(O) sao cho OA=2R.Kẻ hai tiếp tuyến AB,AC với (O)(B;C là các tiếp điểm) . AO cắt BC tại I:
a) Tính theo R hai đoạn thẳng OI và BC.
b) H là điểm nằm giữa I và B(H khác B,I).Đường vuông góc với OH tại H cắt AB,AC tại M và N. CM: Các tứ giác OHBM,OHNC nội tiếp
c)CM: H là trung điểm của MN. Cho H là trung điểm IB. Tính theo R diện tích tam giác OMN