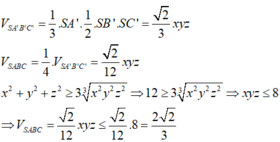Tìm các giá trị của x, y, z thỏa mãn đồng thời:
x + y + z =6 và x2 + y2 + z2= 12
![❄Đờ[̲̅i̲̅]❤Là❤Bể❤K[̲̅h̲̅...](https://hoc24.vn/images/avt/avt2782456_256by256.jpg)
Những câu hỏi liên quan
Cho các số x, y, z thỏa mãn đồng thời:x+y+z=1, x2+y2+z2=1,x3+y3+z3=1 Tính giá trị của biểu thức M=x8+y11+z2018
Cho x; y; z ≠ 0 thỏa mãn x + y + z 0. Tính giá trị biểu thức: A
x
y
x
2
+
y
2
−
z
2
+
y
z
y
2
+...
Đọc tiếp
Cho x; y; z ≠ 0 thỏa mãn x + y + z = 0. Tính giá trị biểu thức: A = x y x 2 + y 2 − z 2 + y z y 2 + z 2 − x 2 + z x z 2 + x 2 − y 2
A. A = 1 2
B. A = - 1 2
C. A = - 3 2
D. A = 3 2
Cho 3 số thực dương x, y, z thỏa mãn:
1
x
2
+
1
y
2
+
1
z
2
1
. Tìm giá trị nhỏ nhất của biểu thức:
P
y
2
z
2
x
(
y
2...
Đọc tiếp
Cho 3 số thực dương x, y, z thỏa mãn: 1 x 2 + 1 y 2 + 1 z 2 = 1 . Tìm giá trị nhỏ nhất của biểu thức: P = y 2 z 2 x ( y 2 + z 2 ) + z 2 x 2 y ( z 2 + x 2 ) + x 2 y 2 z ( x 2 + y 2 )
Ta có:
P = 1 x ( 1 z 2 + 1 y 2 ) + 1 y ( 1 z 2 + 1 x 2 ) + 1 z ( 1 x 2 + 1 y 2 )
Đặt: 1 x = a ; 1 y = b ; 1 z = c thì a,b,c>0 và a2+b2+c2=1
P = a b 2 + c 2 + b c 2 + a 2 + c a 2 + b 2 = a 2 a ( 1 − a 2 ) + b 2 b ( 1 − b 2 ) + c 2 c ( 1 − c 2 )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có:
a 2 1 - a 2 2 = 1 2 .2 a 2 ( 1 − a 2 ) ( 1 − a 2 ) ≤ 1 2 2 a 2 + 1 − a 2 + 1 − a 2 3 = 4 27 = > a ( 1 − a 2 ) ≤ 2 3 3 < = > a 2 a ( 1 − a 2 ) ≥ 3 3 2 a 2 ( 1 )
Tương tự: b 2 b ( 1 − b 2 ) ≥ 3 3 2 b 2 ( 2 ) ; c 2 c ( 1 − c 2 ) ≥ 3 3 2 c 2 ( 3 )
Từ (1); (2); (3) ta có P ≥ 3 3 2 ( a 2 + b 2 + c 2 ) = 3 3 2
Đẳng thức xảy ra a = b = c = 1 3 h a y x = y = z = 3
Vậy giá trị nhỏ nhất của P là 3 3 2
Đúng 0
Bình luận (0)
cho x, y, z ≥ 0 thỏa mãn x + y + z =6. Tìm GTNN và GTLN của
A = x2 + y2 + z2
Bạn tham khảo lời giải tại đây:
cho \(x,y,z\ge0\) thỏa mãn \(x y z=6\). tìm GTLN và GTNN của biểu thức \(A=x^2 y^2 z^2\) - Hoc24
Đúng 0
Bình luận (0)
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện
x
2
+
y
2
+
z
2
1
. Giá trị nhỏ nhất của biểu thức
P
x
y
+
y
z
+
2
x
z...
Đọc tiếp
Cho các số thực x, y, z thay đổi và thỏa mãn điều kiện x 2 + y 2 + z 2 = 1 . Giá trị nhỏ nhất của biểu thức P = x y + y z + 2 x z 2 − 8 x + y + z 2 − x y − y z + 2
A. min P = − 5
B. min P = 5
C. min P = 3
D. min P = − 3
Đáp án D
Ta có C 12 1 . C 10 1 = 120
Khi đó C 12 1 . C 10 1 = 120 . Đặt C 12 1 . C 10 1 = 120
Ta luôn có C 12 1 . C 10 1 = 120
C 12 1 . C 10 1 = 120 Suy ra C 12 1 . C 10 1 = 120
Xét hàm số f t = t 2 − 8 t + 3 trên khoảng − 1 ; + ∞ ,có f ' t = 2 t + 1 2 t + 4 t + 3 2 > 0 ; ∀ t > − 1
Hàm số f(t) liên tục trên − 1 ; + ∞ ⇒ f t đồng biến trên − 1 ; + ∞
Do đó, giá trị nhỏ nhất của f(t) là min − 1 ; + ∞ f t = f − 1 = − 3 . Vậy P min = − 3
Đúng 0
Bình luận (0)
Với x; y; z là các số thực thỏa mãn x + y + z + xy + yz + zx 6. Tìm giá trị nhỏ nhất của biểu thức:
P
4
+
x
4
+
4
+
y
2
+
4
+
z
2
A.
P
min
5...
Đọc tiếp
Với x; y; z là các số thực thỏa mãn x + y + z + xy + yz + zx = 6. Tìm giá trị nhỏ nhất của biểu thức: P = 4 + x 4 + 4 + y 2 + 4 + z 2
A. P min = 5
B. P min = 3 5
C. P min = 5 3
D. P min = 3
z√(12+x2)(12+y2)12+z2
Đọc tiếp
Đề lỗi công thức rồi. Bạn xem lại.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có độ dài các cạnh SABCx, SBACy, SCABz thỏa mãn
x
2
+
y
2
+
z
2
12
. Giá trị lớn nhất của thể tích khối chóp S.ABC là: A.
V
2
2
3
B.
V...
Đọc tiếp
Cho hình chóp S.ABC có độ dài các cạnh SA=BC=x, SB=AC=y, SC=AB=z thỏa mãn x 2 + y 2 + z 2 = 12 . Giá trị lớn nhất của thể tích khối chóp S.ABC là:
A. V = 2 2 3
B. V = 2 3 3
C. V = 2 3
D. V = 3 2 2
Đáp án A
Thể tích khối chóp S.ABC là:
V S . A B C = 2 12 . x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
Mà: x 2 + y 2 − z 2 y 2 + z 2 − x 2 x 2 + z 2 − y 2
≤ x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + x 2 + z 2 − y 2 27
= x 2 + y 2 + z 2 3 27
Suy ra: S . A B C ≤ 2 12 . x 2 + y 2 + z 2 27
= 2 12 . 12 3 27 = 2 2 3
Vậy: V max = 2 2 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có độ dài các cạnh:
S
A
B
C
x
,
S
B
A
C
y
,
S
C
A
B
z
thỏa mãn
x
2
+
y
2
+
z
2
12
. Tính giá trị lớn nhất của thể...
Đọc tiếp
Cho hình chóp S.ABC có độ dài các cạnh: S A = B C = x , S B = A C = y , S C = A B = z thỏa mãn x 2 + y 2 + z 2 = 12 . Tính giá trị lớn nhất của thể tích khối chóp S.ABC.
A. 2 3
B. 8 3
C. 2 2 3
Đáp án C
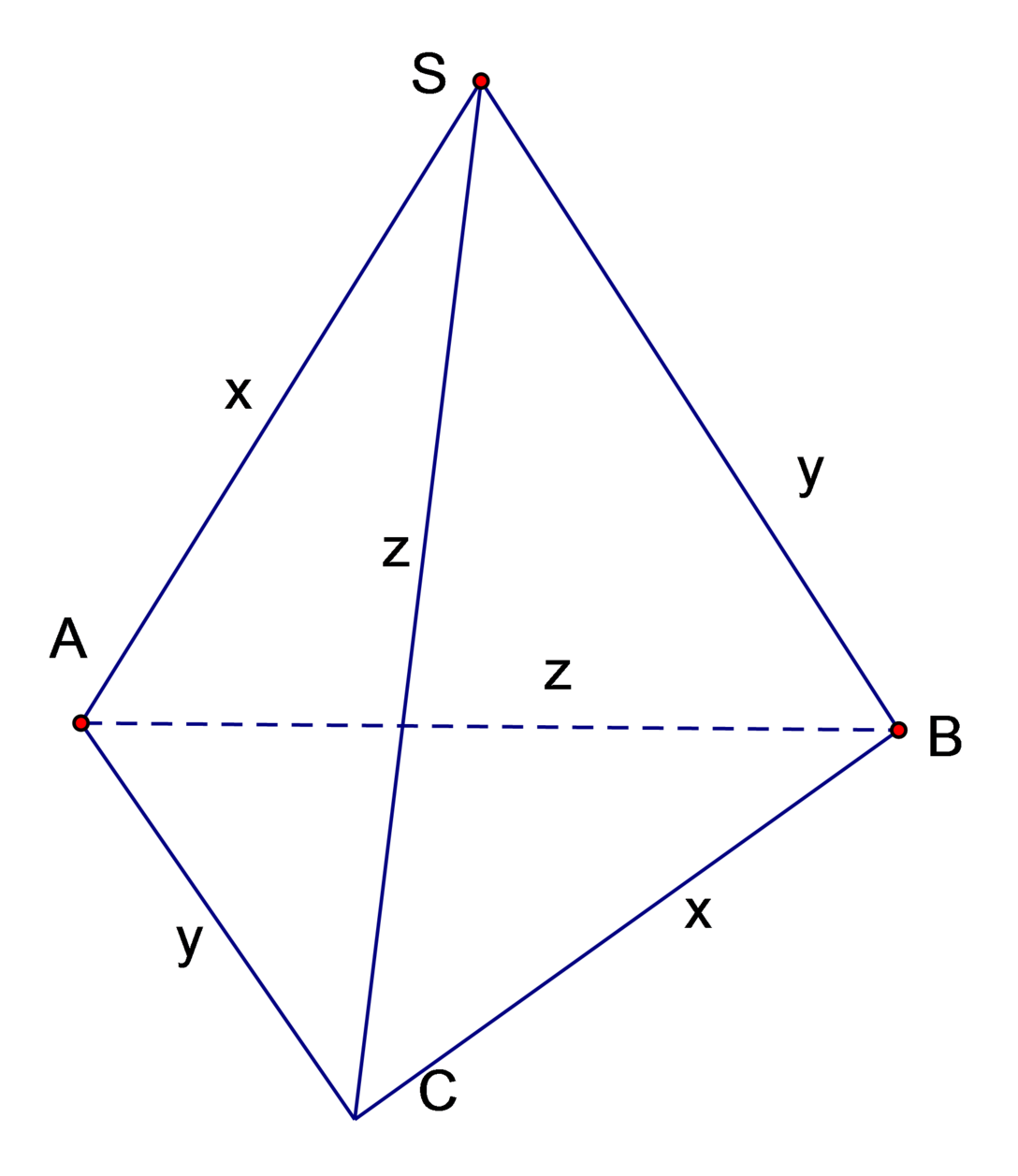
Áp dụng công thức tính thể tích tứ diện có hai cặp cạnh đối bằng nhau:
V S A B C = 1 6 2 x 2 + y 2 − z 2 y 2 + z 2 − x 2 z 2 + x 2 − y 2 ≤ 1 6 2 x 2 + y 2 − z 2 + y 2 + z 2 − x 2 + z 2 + x 2 − y 2 3 3 = 1 6 2 x 2 + y 2 + z 2 3 3 = 1 6 2 12 3 3 = 1 6 2 .8 = 2 2 3
Như vậy V S A B C lớn nhất bằng 2 2 3 khi: x=y=z=2
Đúng 0
Bình luận (0)
Cho hình chóp S. ABC có độ dài các cạnh SA SB x, SB SC y, SC AB z thỏa mãn
x
2
+
y
2
+
z
2
12
. Tính giá trị lớn nhất của thể tích khối chóp S. ABC.
Đọc tiếp
Cho hình chóp S. ABC có độ dài các cạnh SA = SB = x, SB = SC = y, SC = AB= z thỏa mãn x 2 + y 2 + z 2 = 12 . Tính giá trị lớn nhất của thể tích khối chóp S. ABC.
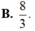
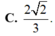
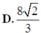
Đáp án C
Dựng hình chóp SA’B’C’ sao cho A là trung điểm A’B’, B là trung điểm B’C’, C là trung điểm A’C’.
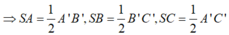
Suy ra SA’,SB’,SC’ đôi một vuông góc với nhau
Đúng 0
Bình luận (0)