Luôn có vô số nghiệm

\(\left\{{}\begin{matrix}y=\frac{3x}{18}\\x=\frac{18y}{3}\end{matrix}\right.\)

Vẽ đường thẳng (d): -3x + 2y = 0

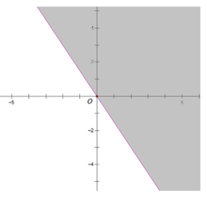
Lấy điểm A(1; 1), ta thấy A ∉(d) và có: -3.1 + 2.1 < 0 nên nửa mặt phẳng bờ (d) không chưá A là miền nghiệm của bất phương trình. (miền hình không bị tô đậm)

Câu 1: C

Câu 3: D

Câu 4: A

Câu 8: A

a) \(5x + 3y < 20\)

Đây là bất phương trình bậc nhất hai ẩn.

Chọn \(x = 0;y = 0\)

Khi đó bất phương trình tương đương với 5.0+3.0

Vậy (0;0) là một nghiệm của bất phương trình trên.

b) \(3x - \frac{5}{y} > 2\)

Đây không là bất phương trình bậc nhất hai ẩn vì có ẩn y ở mẫu.

Ta có: 3x – 2y = 5 ⇔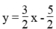 

Để được một hệ có nghiệm duy nhất thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc khác 3/2 .

Chẳng hạn: 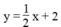 ⇔ -x + 2y = 4

Khi đó ta có hệ 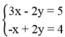 có một nghiệm duy nhất.

Ta có: 3x – 2y = 5 ⇔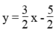 

Để được một hệ có vô số nghiệm thì cần thêm một phương trình bậc nhất hai ẩn có hệ số góc bằng 3/2 và tung độ gốc bằng - 5/2 .

Chẳng hạn: 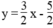 ⇔ 6x – 4y = 10

Khi đó ta có hệ 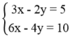 có vô số nghiệm.

Một phương trình bậc nhất một ẩn luôn có một nghiệm duy nhất.

(lưu ý vì đây là phương trình bậc nhất một ẩn nên a ≠ 0, do đó phương trình luôn có một nghiệm duy nhất. Không có trường hợp a = 0.)

Chọn đáp án B.

Bước 1: Mở trang Geoebra

Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô

Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).

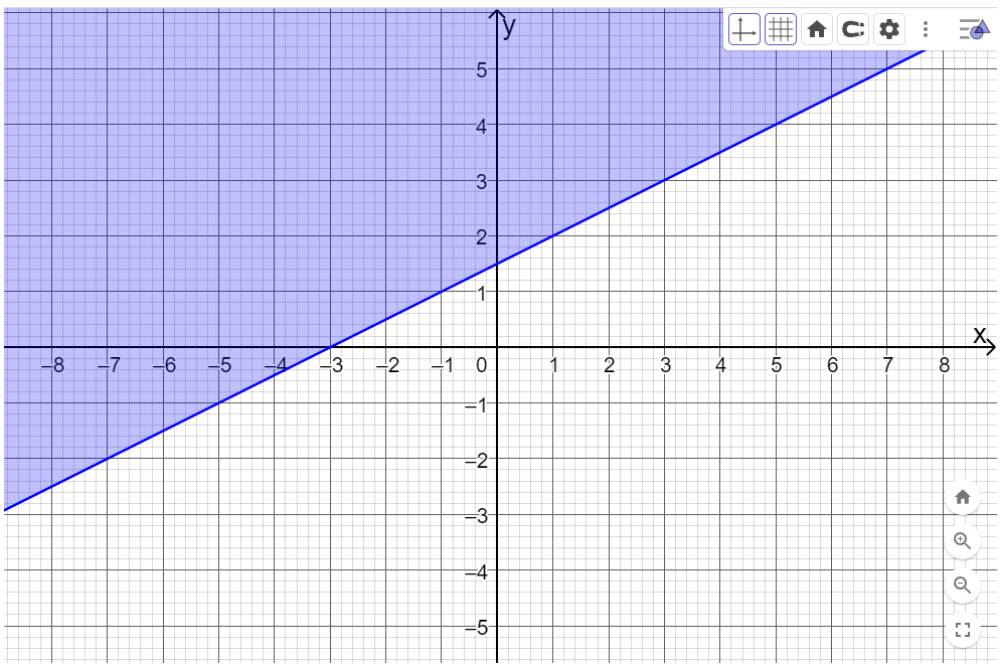
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:

x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.

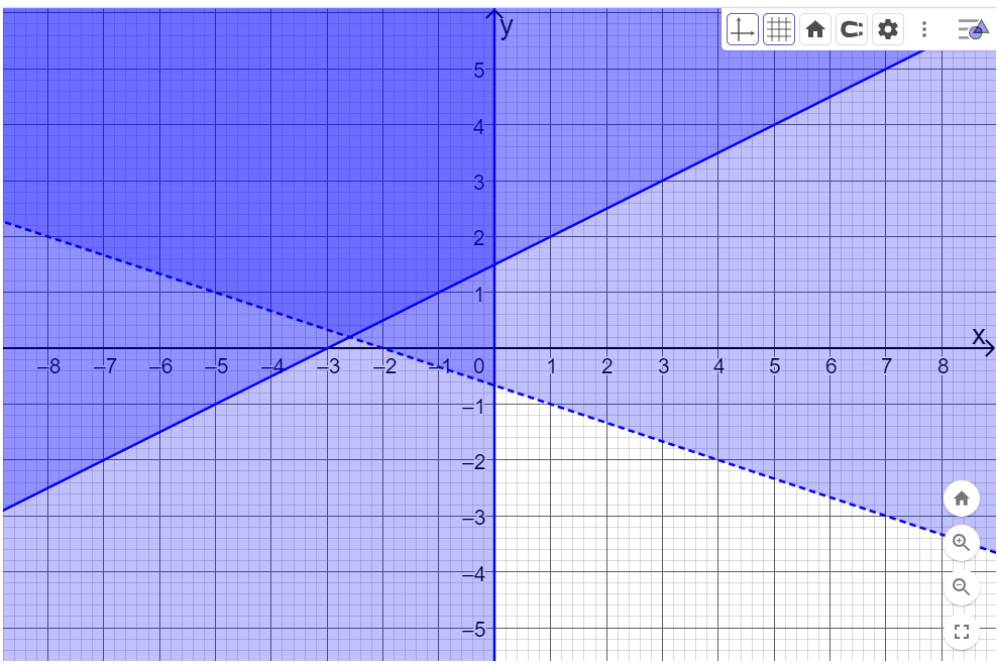
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y =  - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.