M=1+1/5+3/35+...+3/9603+3/9999

Những câu hỏi liên quan
tính tổng \(M=1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)
\(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{35}+\dfrac{2}{63}+...+\dfrac{2}{9603}+\dfrac{2}{9999}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{97}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\cdot\dfrac{96}{505}=\dfrac{150}{101}\)
Đúng 1
Bình luận (0)
Tìm M : M= 1/3+13/15+33/35+...+9601/9603+9997/9999
☹➞cac ban giup minh cau nay voi
☛ tinh tong
M = 1+\(\dfrac{1}{5}\)+\(\dfrac{3}{35}\)+...\(\dfrac{3}{9603}\)+\(\dfrac{3}{9999}\)
➜giup minh nhanh nhe minh dang can gap lam moi nguoi a
➞thank you cac ban ❕
\(M=1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9999}\\ =\dfrac{3}{3}+\dfrac{3}{15}+\dfrac{3}{35}+...+\dfrac{3}{9999}\\ =\dfrac{3}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{99\cdot101}\right)\\ =\dfrac{3}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{99}-\dfrac{1}{101}\right)\\ =\dfrac{3}{2}\left(1-\dfrac{1}{101}\right)=\dfrac{3}{2}\cdot\dfrac{100}{101}=\dfrac{150}{101}\)
Đúng 1
Bình luận (0)
a, Tính: M = \(1+\dfrac{1}{5}+\dfrac{3}{35}+...+\dfrac{3}{9603}+\dfrac{3}{9999}\)
b, Chứng tỏ: S = \(\dfrac{1}{4^2}+\dfrac{1}{6^2}+\dfrac{1}{8^2}+...+\dfrac{1}{\left(2n\right)^2}< \dfrac{1}{4}\left(n\in N,n\ge2\right)\)
a: \(M=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{2}{5\cdot7}+...+\dfrac{2}{97\cdot99}+\dfrac{2}{99\cdot101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{2}\left(\dfrac{1}{5}-\dfrac{1}{101}\right)\)
\(=\dfrac{6}{5}+\dfrac{3}{10}-\dfrac{3}{202}=\dfrac{150}{101}\)
b: 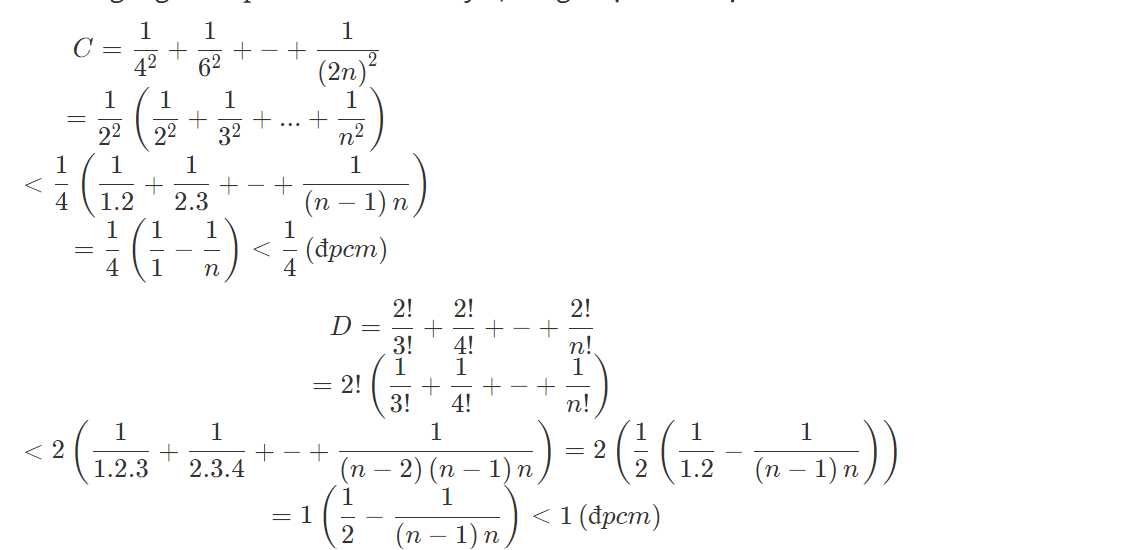
Đúng 1
Bình luận (0)
tính nhanh 1/3 + 13/15 + 33/35 + 61/65 +......+ 9601/9603+ 9997/9999
1/3+13/15+33/35+61/62+...+9601/9603+9997/9999
Hình như đề bài nhầm thì phải: 61/63 chứ?
Đúng 0
Bình luận (0)
1/3+13/15+33/35+31/63+.....................+9601/9603+9997/9999
cứu với
1/3+13/15+33/35+31/63+.....................+9601/9603+9997/9999
\(=1-\frac{2}{3}+1-\frac{2}{15}+...+1-\frac{2}{9999}\)
\(=\left(1+1+1+1+...+1\right)-\left(\frac{2}{3}+\frac{2}{15}+\frac{2}{35}+...+\frac{2}{9999}\right)\)
\(=50-\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{99.101}\right)\)
\(=50-\left(1-\frac{1}{101}\right)=50-\frac{100}{101}=\frac{4950}{101}\)
HTDT
Đúng 0
Bình luận (0)
\(1005+\frac{1}{3}+\frac{1}{15}+\frac{1}{35}+...+\frac{1}{9603}+\frac{1}{9999}\)
1005\(\frac{49}{303}\)
tính
1/3+13/15+33/35+61/63+...+9601/9603+9997/9999
tl nhanh jup mik, đag cần gấp
\(\frac{1}{3}+\frac{13}{15}+...+\frac{9997}{9999}\)
\(=1-\frac{2}{3}+1-\frac{2}{15}+...+1-\frac{2}{9999}\)
\(=\left(1+1+...+1\right)-\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{99.101}\right)\)
\(=50-\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{99}-\frac{1}{101}\right)\)
\(=50-\left(1-\frac{1}{101}\right)\)
Sau bạn tính tiếp là OK rồi
Đúng 0
Bình luận (0)



















