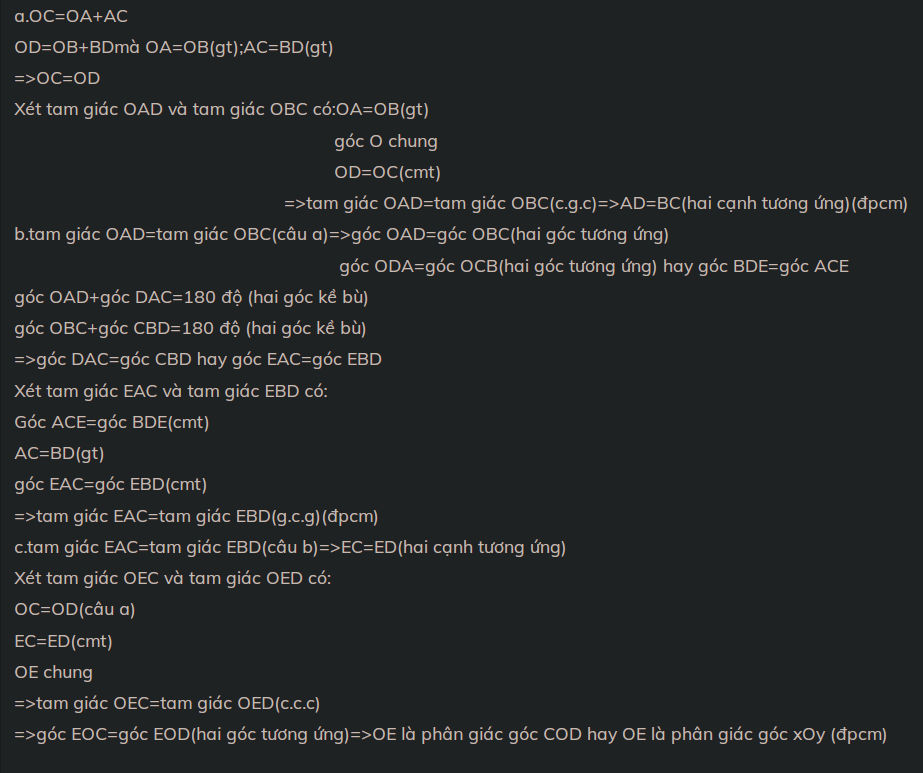
1. Cho \(\widehat{xOy}\)nhọn. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA=OB ( A và B khác O ). Lấy điểm C nằm giữa 2 điểm O và A, lấy điểm D trên tia By sao cho BD=AC. Gọi I là giao điểm của AB và CD. Qua C kẻ đường thẳng song song với Oy cắt AB tại M.
a) CMR: \(\Delta\)CAM là \(\Delta\)cân.
b) CMR: I là trung điểm CD.
c) Đường thẳng vuông góc với CD tại I và tia phân giác của \(\widehat{xOy}\)cắt nhau tại H. CMR: HB \(\perp\)Oy.
2. Cho \(\Delta\)ABC (AB<AC, \(\widehat{B}\)= 60o). 2 tia phân giác AD (D\(\in\)BC) và CE ( E \(\in\)AB) của \(\Delta\)ABC cắt nhau tại I. CMR: \(\Delta\)IDE cân.
Nhờ mọi người giúp mình. Không cần vẽ hình, chỉ cần giải giúp mình là được. Mình cảm ơn