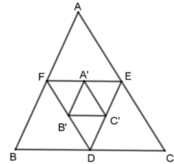
Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên E F B C = F D A C = E D A B = 1 2  suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.

Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ đồng dạng ΔDEF theo tỉ số k = 1 2

Theo tính chất đường trung bình B ' C E F = 1 2 mà E F B C = 1 2 (cmt) suy ra  B ' C ' B C = 1 4

Tương tự  A ' B ' A B = A ' C ' A C = 1 4

Do đó ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 4

Đáp án: C

a: Xét tứ giác ADCF có 

E là trung điểm của AC

E là trung điểm của DF

Do đó: ADCF là hình bình hành

Suy ra: AD//CF và AD=CF

=>BD=CF và BD//CF

Xét ΔBDC và ΔFCD có

\(\widehat{BDC}=\widehat{FCD}\)

DC chung

\(\widehat{BCD}=\widehat{FDC}\)

Do đó:ΔBDC=ΔFCD

b: Xét ΔACB có

D là trung điểm của AB

E là trung điểm của AC

Do đó: DE là đường trung bình của ΔABC

Suy ra: DE//BC và DE=1/2BC

a)Ta có : AB = AC
=> △ ABC cân tại A
Xét △ ABC cân tại A có : 
AD là đường trung tuyến 
=> AD là đường phân giác
Xét △ ADE vuông tại E và △ ADF vuông tại F có :
AD là cạnh chung
DAEˆ=DAFˆDAE^=DAF^ ( AD là đường phân giác )
Vậy △ ADE = △ ADF (ch-gn)
=> AE = AF ( hai cạnh tương ứng )
=> A nằm trên đường trung trực của EF (1)
Lại có : DE = DF ( △ ADE = △ ADF )
=> D nằm trên đường trung trực của EF (2)
Từ (1), (2) => AD là đường trung trực của EF

Mấy câu sau bạn tự làm nhé

tự kẻ hình nha:333

a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)

xét tam giác MAB và tam giác  DAB có

MH=HD(cmt)

AHM=AHD(=90 độ)

AH chung

=> tam giác MAB= tam giác DAB(cgc)

=> AM=AD( hai cạnh tương ứng)

vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)

xét tam giác AKD và tam giác AKN có

DK=NK(cmt)

AKD=AKN(=90 độ)

AK chung

=> tam giác AKD= tam giác AKN( cgc)

=> AN=AD ( hai cạnh tương ứng)

AM=AD(cmt)

=> AM=AN=> tam giác AMN cân A

b) vì E thuộc đường trung trực AB=> EM=ED

vì F thuộc đường trung trực AC=> FD=FN

ta có MN=ME+EF+FN mà EM=ED, FD=FN

=> MN= ED+EF+FD

c) xét tam giác ADF và tam giác ANF có

FD=FN(cmt)

AD=AN(cmt)

AF chung

=> tam giác ADF= tam giác ANF(ccc)

=> ANF=ADF( hai góc tương ứng)

xét tam giác AME và tam giác ADE có

AM=AD(cmt)

AE chung

EM=ED(cmt)

=> tam giác AME= tam giác ADE(ccc)

=> AME=ADE( hai góc tương ứng)

mà AME=ANF( tam giác AMN cân A)

=> ADE=ADF=> AD là p/g của EDF

d) chưa nghĩ đc :)))))))

CHUẨN R BN ƠI HỌC THÌ NGU MÀ CHƠI NGU THÌ GIỎI