giải hệ phương trình ax-y=a^2-a và (a+1)x+ay=2a-1

Những câu hỏi liên quan
Cho hệ phương trình :hept{begin{cases}ax-y2ax-ay3+aend{cases}}(a là tham số )a) giải hệ phương trình theo a. Áp dụng tìm nghiệm khi a 1-sqrt{2}b) Tìm a để hệ phương trình có nghiệm duy nhất thỏa mãn x+yfrac{a^2-5}{a-1}c) Tìm a inZ để hệ phương trình có nghiệm duy nhất (x;y) nguyên . Tìm giá trị các nghiệm nguyên đó
Đọc tiếp
Cho hệ phương trình :\(\hept{\begin{cases}ax-y=2a\\x-ay=3+a\end{cases}}\)(a là tham số )
a) giải hệ phương trình theo a. Áp dụng tìm nghiệm khi a =\(1-\sqrt{2}\)
b) Tìm a để hệ phương trình có nghiệm duy nhất thỏa mãn \(x+y=\frac{a^2-5}{a-1}\)
c) Tìm a \(\in\)Z để hệ phương trình có nghiệm duy nhất (x;y) nguyên . Tìm giá trị các nghiệm nguyên đó
Cho hệ pt: ax+ y= 2a X-a= 1-ay 1/ a=2 giải hệ pt 2/ tìm a để a/ hệ có 1 nghiệm duy nhất, vô số nghiệm, vô nghiệm B/ hệ có nghiệm nguyên
a: \(\left\{{}\begin{matrix}ax+y=2a\\x-a=1-ay\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}ax+y=2a\\x+ay=a+1\end{matrix}\right.\)
Khi a=2 thì hệ sẽ là \(\left\{{}\begin{matrix}2x+y=4\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=4\\2x+4y=6\end{matrix}\right.\)
=>-3y=-2 và x+2y=3
=>y=2/3 và x=3-2y=3-4/3=5/3
2:
a: Để hệ có 1 nghiệm duy nhất thì \(\dfrac{a}{1}< >\dfrac{1}{a}\)
=>a^2<>1
=>a<>1 và a<>-1
Để hệ có vô số nghiệm thì \(\dfrac{a}{1}=\dfrac{1}{a}=\dfrac{2a}{a+1}\)
=>a^2=1 và a^2+a=2a
=>a=1
Để hệ vô nghiệm thì \(\dfrac{a}{1}=\dfrac{1}{a}< >\dfrac{2a}{a+1}\)
=>a^2=1 và a^2+a<>2a
=>a=-1
Đúng 0
Bình luận (0)
Cho hệ phương trình: x+ay=2 và ax-27=1. Tìm các giá trị của a để hệ phương trình đã cho có nghiệm thỏa mãn điều kiện x>0, y<0.
Cho hệ phương trình:
x + ay = 1 Và. -ax + y = a
Chứng minh hệ phương trình luôn có nghiẹm với mọi a
Giá trị của a để hệ phương trình
x
+
a
y
1
−
a
x
+
y
a
có nghiệm
x...
Đọc tiếp
Giá trị của a để hệ phương trình x + a y = 1 − a x + y = a có nghiệm x < 1 y < 1 là:
A. a = 1
B. a = 0
C. a = 0; a = 1
D. a ≠ 0; a ≠ 1
x + a y = 1 − a x + y = a ⇔ x = 1 − a y − a 1 − a y + y = a ⇔ x = 1 − a y y a 2 + 1 = 2 a ⇔ x = 1 − a y y = 2 a a 2 + 1 ⇔ x = 1 − a 2 a 2 + 1 y = 2 a a 2 + 1
Để hệ phương trình đã cho có nghiệm thỏa mãn: x < 1; y < 1
⇒ 1 − a 2 a 2 + 1 < 1 2 a a 2 + 1 < 1 ⇔ 1 − a 2 < a 2 + 1 2 a < a 2 + 1 ⇔ 2 a 2 > 0 a − 1 2 > 0 ⇔ a ≠ 0 a ≠ 1
Đáp án:D
Đúng 0
Bình luận (0)
cho hệ phương trình \(\hept{\begin{cases}x+ay=1\\ax+y=2\end{cases}}\)
a) giải hệ khi a=2
b)với giá trị nào của a thì hệ có nghiệm duy nhất
Cho hệ Phương trình x+ay=1 và -ax+y=a
a)Chứng minh rằng hệ luôn luôn có no duy nhất với mọi a
b)Tìm a để hệ có nghiệm (x,y) sao cho x<1 ; y<1
Lời giải:
a) $x+ay=1\Rightarrow x=1-ay$. Thay vào PT $(2)$ có:
$-a(1-ay)+y=a$
$\Leftrightarrow y(1+a^2)=2a(*)$
Vì $1+a^2\neq 0$ với mọi $a\in\mathbb{R}$ nên PT $(*)$ có nghiệm $y=\frac{2a}{a^2+1}$ duy nhất.
Kéo theo HPT ban đầu có nghiệm $(x,y)$ duy nhất với mọi $a$
b) $y=\frac{2a}{a^2+1}$ nên $x=1-ay=1-\frac{2a^2}{a^2+1}=\frac{1-a^2}{a^2+1}$
Để \(x< 1; y< 1\Leftrightarrow \left\{\begin{matrix} \frac{2a}{a^2+1}< 1\\ \frac{1-a^2}{a^2+1}< 1\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 2a< a^2+1\\ 1-a^2< a^2+1\end{matrix}\right.\)
\(\Leftrightarrow \left\{\begin{matrix} a^2+1-2a>0\\ 2a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} (a-1)^2>0\\ a^2>0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a\neq 1\\ a\neq 0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hệ phương trình:
\(\hept{\begin{cases}x+ay=a+1\\ax+y=3a-1\end{cases}}\)
a) Giải hệ trên với a = \(\sqrt{3}-1\)
b) Giải và biện luận hệ trên
c) Tìm a để phương trình có nghiệm nguyên duy nhất và xy đạt GTNN
♥ Các bạn giải nhanh cho mình nhé ♥
Phần tự luận
Nội dung câu hỏi 1
Cho hệ phương trình : x + a y = 3 a x - y = 2
a) Giải hệ phương trình khi a = 2
a) Khi a = 2, ta có hệ phương trình
![]()
![]()
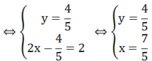
Vậy hệ phương trình có nghiệm duy nhất (x; y) = (7/5; 4/5)
Đúng 0
Bình luận (0)













