chứng minh 0=1?????
không chứng minh theo kiểu 0 x 0 = 1 x 0
Những câu hỏi liên quan
1. chứng minh x4 - x + 1 = 0 vô nghiệm
2. chứng minh x4 - x2 + 1 = 0 vô nghiệm
3. chứng minh x4 - x3 + 1 = 0 vô nghiệm
4. chứng minh a2 + \(\dfrac{1}{a^2}\)
biết a khác 0
2) \(x^4-x^2+1=0\)(1)
Đặt: t=x2, khi đó:
(1)\(\Leftrightarrow t^2-t+1=0\)
\(\Leftrightarrow\left(t-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\left(2\right)\)
\(\Rightarrow\left(2\right)\) vô nghiệm => (1) vô nghiệm
Đúng 0
Bình luận (0)
Chứng minh rằng không đồng thời tồn tại x+y+z=0 và 1/x+1/y+1/z=0
cho f (x ) = ax2 + bx + c ( a, b,c khác 0 và a + 3b + 6c = 0
a, tìm a , b ,c theo f(0) , f ( 1 / 2 ) ,f ( - 1 )
b chứng minh f (0) , f( 1 / 2 ) , f( - 1) không thể cùng âm hoặc cungf dương
Cho hai phương trình:
5
x
2
+
3
x
−
8
0
(1) và
−
x
2
+
8
x
−
7
0
(2)a) Chứng minh x1 là nghiệm chung của hai phương trình (1) và (2).b) Chứng minh
x
−
8
5
là nghiệm của (1) nhưng không là nghiệm của (2).c) Hai...
Đọc tiếp
Cho hai phương trình: 5 x 2 + 3 x − 8 = 0 (1) và − x 2 + 8 x − 7 = 0 (2)
a) Chứng minh x=1 là nghiệm chung của hai phương trình (1) và (2).
b) Chứng minh x = − 8 5 là nghiệm của (1) nhưng không là nghiệm của (2).
c) Hai phương trình đã cho có tương đương không? Vì sao?
a,Cho đa thức f(x)=ax+b (a khác 0). Biết f(0)=0, chứng minh rằng F(x)=-f(-x)với mọi x
b,Đa thức f(x)=ax^2=bx+c (a khác 0).Biết F(1)=F(-1), chứng minh rằng f(x) với mọi x
Chứng minh rằng hàm số f(x) = cos(1/x) không có giới hạn khi x → 0
Chọn hai dãy số có số hạng tổng quát l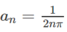à 
và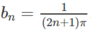 
.
Tính và so sánh lim f ( a n ) và lim f ( b n ) để kết luận về giới hạn của f(x) khi x → 0
Đúng 0
Bình luận (0)
ĐK: x≥0, x khác 1 Chứng minh rằng 0<A<2
Cho 0 ≤ x , y ≤ 1 0≤x,y≤1. Chứng minh x√y − y√x≤1/4
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
Đúng 0
Bình luận (0)
Chứng minh rằng nếu x>0 thì 1/x - 1/(x+1)>0
ơi STN = số thứ nhất
STH = SỐ THỨ 2 NHÉ
STB = SỐ THỨ 3 NHA
Chứng minh rằng nếu \(x>0\)thì \(\frac{1}{x}-\frac{1}{x+1}>0\):
Ta có : \(\frac{1}{x}-\frac{1}{x+1}>0\Rightarrow\frac{1}{x}>\frac{1}{x+1}\)
\(\Rightarrow x+1>x\)(đúng)
Học tốt