Bài 1: Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB. CM: \(S_{ABCD}=2S_{ECD}\)

Những câu hỏi liên quan
Cho hình chữ nhật ABCD, E là điểm tùy ý trên AB.
Chứng minh rằng: S A B C D = 2 S E C D
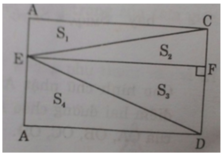
Kẻ EF ⊥ CD ⇒ AC // EF // AD
Xét ΔBCE và ΔFEC có:
(CAE) = (CFE) = 90o
(BCE) = (CEF) (Hai góc so le trong)
CE chung
⇒ ΔBCE = ΔFEC (cạnh huyền- góc nhọn)
tương tự ΔAED=ΔFDE.
Do đó (theo hình vẽ):
S1 = S2 và S3 = S4
⇒ S2 + S3 = S1 + S4 = (1/2)SABCD
Hay SECD = (1/2)SABCD ⇒ SABCD = 2SECD.
Đúng 0
Bình luận (0)
1. cho hình chữ nhật ABCD, E là điểm tùy ý trên cạnh AB. chứng minh SABCD = 2.SEDC
mọi người giúp nhé!!!
cho hình chữ nhật ABCD , E là điểm tùy ý trên AB. chứng minh SABCD = 2SEDC
cho hình chữ nhật ABCD. M là điểm trên cạnh AB. CMR: \(S_{ABCD}=2S_{MDC}\)
cho hình chữ nhật ABCD có chiều dài CD = 27 cm , chiều rộng AD= 20,4. E là một điểm trên cạnh AB . tính diện tích tam giác ECD
Diện tích hình chữ nhật là :
27 . 20,4 = 550,8 \(cm^2\)
Chiều cao = Chiều rộng
Chiều dài là Đày hình tam giác
Diện tích hình tam giác là :
550,8 : 2 = 275,4 \(cm^2\)
Đáp số : 275,4 \(cm^2\)
Đúng 0
Bình luận (0)
Diện tích hình chữ nhật là :
27 * 20,4 = 550,8 cm2
Chiều cao = chiều rộng
Chiều dài là đáy hình tam giác
Diện tích hình tam giác ECD là :
550,8 : 2 = 275,4 cm2
Đúng 0
Bình luận (0)
Diện tích hình chữ nhật là :
27 * 20,4 = 550,8 cm2
Chiều cao = chiều rộng
Chiều dài là đáy hình tam giác
Diện tích hình tam giác ECD là :
550,8 : 2 = 275,4 cm2
Đs :.......
Đúng 0
Bình luận (0)
bài 1 cho hình thang ABCD (AB // CD và AB CD ) trên đg AD lấy AE EM MP PD .Trên đg BC lấy BF FN NQ QC .1) C/m M, N lần lượt là trung điểm của AD và BC.2) tứ giác EFQP là hình gì ?3) tính MN ,EF ,PQ biết AB 8 cm và CD 12 cm4) kẻ AH vuông góc tại H và AH 10 cm . tính S_{ABCD}bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD DE EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại M, N . C/m rằng : 1) M là trung điểm của AN.2) AM MN NC .3) 2EN DM + BC .4)S_{ABC}3S_{...
Đọc tiếp
bài 1 cho hình thang ABCD (AB // CD và AB < CD ) trên đg AD lấy AE = EM = MP = PD .Trên đg BC lấy BF = FN = NQ = QC .
1) C/m M, N lần lượt là trung điểm của AD và BC.
2) tứ giác EFQP là hình gì ?
3) tính MN ,EF ,PQ biết AB = 8 cm và CD = 12 cm
4) kẻ AH vuông góc tại H và AH = 10 cm . tính \(S_{ABCD}\)
bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD = DE = EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại M, N . C/m rằng : 1) M là trung điểm của AN.
2) AM = MN = NC .
3) 2EN = DM + BC .
4)\(S_{ABC}=3S_{AMB}\)
bài 3 : cho hình thang ABCD ( AB //CD ) có đg cao AH = 3 cm và AB = 5cm , CD = 8cm gọi E, F , I lần lượt là trung điểm của AD , BC và AC.
1) C/m E ,F ,I thẳng hàng .
2) tính \(S_{ABCD}\)
3) so sánh \(S_{ADC}\) và \(2S_{ABC}\)
bài 4: cho tứ giác ABCD . gọi E, F, I lần lượt là trung điểm AD , BC và AC .1) C/m E, I , F thẳng hàng
2) tính EF≤ AB+CD / 2
3) tứ giác ABCD phải có điều kiện gì thì EF = AB+CD / 2
Cho hình chữ nhật ABCD. Trên AD và BC ta lấy hai điểm M, N sao cho AM = CN. Lấy điểm K tùy ý trên AB, MN cắt KD và KC tại E và F. Chứng tỏ rằng: \(S_{KEF}=S_{MED}+S_{FNC}\)
Mai ơi giúp mk nhé ![]()
Sơ đồ minh họa:
Phân tích: Ta thấy tam giác \(KDC\) và tứ giác \(MNCD\) có phần chung là tứ giác \(EFCD\).
Vậy để chứng tỏ: \(S_{KEF}=S_{MED}+S_{FNC}\) ta cần chứng tỏ \(S_{KDC}=S_{MNCD}\)
Giải tóm tắt:
\(S_{KDC}=DC\times BC\div2=\frac{1}{2}\times S_{ABCD}\) (1)
Vì \(ABCD\) là hình chữ nhật nên tứ giác \(MNCD\) là hình thang và có diện tích là:
\(S_{MNCD}=\left(MD+NC\right)\times DC\div2=\)
\(=AD\times DC\div2=\frac{1}{2}\times S_{ABCD}\) (2)
Từ (1) và (2) ta có: \(S_{KDC}=S_{MNCD}\)
Tam giác \(KDC\) và hình thang \(MNCD\) có phần chung là tứ giác \(EFCD\), suy ra:
\(S_{KEF}=S_{MED}+S_{FNC}\)
Đúng 1
Bình luận (0)
hình chữ nhật ABCD có chiều dài DC là 30 cm chiều rộng AD kém chiều dài 5,6 cm . E là 1 điểm trên đoạn AB tính diện tích hình tam giác ECD
LAM NHANH LEN NHE . THANK YOU CẢ CÁCH LÀM NỮA NHÉ
1,Cho hình thoi ABCD có Â60 độ .VẼ AH vuông góc với AD, trên tia đối của HB lấy điểm E sao cho HEHBa, Cm abde là hình thoib, Ba điểm E,C,D thẳng hàngc, EBAC2, Cho hình chữ nhật abcd. lấy điểm P tùy ý trên đường chéo BD. Gọi M là điểm đối xúng của C qua Pa, CM: AM song song BDb, Gọi E,F lần lượt là hình chiếu của M trên AD,ABc,Cm EF song song ACD, cM E,F,P thẳng hànggiúp e vs mai nộp rồi
Đọc tiếp
1,Cho hình thoi ABCD có Â=60 độ .VẼ AH vuông góc với AD, trên tia đối của HB lấy điểm E sao cho HE=HB
a, Cm abde là hình thoi
b, Ba điểm E,C,D thẳng hàng
c, EB=AC
2, Cho hình chữ nhật abcd. lấy điểm P tùy ý trên đường chéo BD. Gọi M là điểm đối xúng của C qua P
a, CM: AM song song BD
b, Gọi E,F lần lượt là hình chiếu của M trên AD,AB
c,Cm EF song song AC
D, cM E,F,P thẳng hàng
giúp e vs mai nộp rồi
















