8523+8423+2310=

Những câu hỏi liên quan
8423÷3
8423 + 9512 = ???
Ai tk mk thì mk tk lại ( lên điểm )
Xem thêm câu trả lời
Tìm số trung bình cộng của các số lẻ có 4 chữ số bé hơn 8423
Xem chi tiết
Tìm số trung bình cộng của các số lẻ có 4 chữ số bé hơn 8423
Xem chi tiết
lollllllllllll
Chứng minh\(\left(\sqrt{2}+\sqrt{3}\right)^{2310}+\left(\sqrt{2}-\sqrt{3}\right)^{2310}\in Z\)
Ta có:
\(\hept{\begin{cases}\left(\sqrt{2}+\sqrt{3}\right)^2=5+2\sqrt{6}\\\left(\sqrt{2}-\sqrt{3}\right)^2=5-2\sqrt{6}\end{cases}}\)
Ta chứng minh: Với mọi \(n\in N;n>0\)thì \(\left(5+2\sqrt{6}\right)^n+\left(5-2\sqrt{6}\right)^n\in Z\)
Với \(n=1\)thì \(\left(5+2\sqrt{6}\right)^1+\left(5-2\sqrt{6}\right)^1=10\in Z\)
Với \(n=2\)thì \(\left(5+2\sqrt{6}\right)^2+\left(5-2\sqrt{6}\right)^2=98\in Z\)
Giả sử nó đúng đến \(n=k\)hay
\(\left(5+2\sqrt{6}\right)^k+\left(5-2\sqrt{6}\right)^k=a\in Z\)
Ta chứng minh nó đúng với \(n=k+1\) hay \(\hept{\begin{cases}\left(5+2\sqrt{6}\right)^{k-1}+\left(5-2\sqrt{6}\right)^{k-1}=a\in Z\\\left(5+2\sqrt{6}\right)^k+\left(5-2\sqrt{6}\right)^k=b\in Z\end{cases}}\)
Ta có:
\(\left(5+2\sqrt{6}\right)^{k+1}+\left(5-2\sqrt{6}\right)^{k+1}\) \(=\left(5+2\sqrt{6}\right).\left(5+2\sqrt{6}\right)^k+\left(5-2\sqrt{6}\right).\left(5-2\sqrt{6}\right)^k\)
\(=\left(5+2\sqrt{6}\right).\left(b-\left(5-2\sqrt{6}\right)^k\right)+\left(5-2\sqrt{6}\right).\left(b-\left(5+2\sqrt{6}\right)^k\right)\)
\(=b\left(\left(5+2\sqrt{6}\right)+\left(5-2\sqrt{6}\right)\right)-\left(5+2\sqrt{6}\right).\left(5-2\sqrt{6}\right)^k-\left(5-2\sqrt{6}\right).\left(5+2\sqrt{6}\right)^k\)
\(=10b-\left(5-2\sqrt{6}\right)^{k-1}-\left(5+2\sqrt{6}\right)^{k-1}\)
\(=10b-a\in Z\)
Vậy theo quy nạp thì nó đúng.
Quay lại bài toán thì ta có:
\(\left(\sqrt{2}+\sqrt{3}\right)^{2310}+\left(\sqrt{2}-\sqrt{3}\right)^{2310}=\left(5+2\sqrt{6}\right)^{1155}+\left(5-2\sqrt{6}\right)^{1155}\in Z\)
Đúng 0
Bình luận (0)
4441+2310=?
4 441 + 2 310 = 6 751
k nha ^_-
( đưng trừ điểm )
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Tìm X biết 18x2310+2310x81+2310=X.1000
Tìm các ước nguyên tố của các số 30, 210, 2310
Phân tích các số đó cho thành tích các thừa số nguyên tố
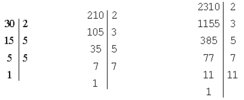
Ta có:
- Ước nguyên tố(30) = {1, 2, 3, 5}
Và 30 = 1.2.3.5
- Ước nguyên tố(210) = {1, 2, 3, 5,7}
Và 210 = 1.2.3.5.7
- Ước nguyên tố(2310) = {1, 2, 3, 5, 7, 11}
Và 30 = 1.2.3.5.7.11
Chỳ ý: Khi phân tích số 210 ra thừa số nguyên tố ta có thể làm như sau :
210 = 21.10 . Ta đó biết 10 = 2.5 nên chỉ cần phân tích 21 = 3.7 và có
210 = 2.7.2.5
Cách này hoàn toàn có lợi khi phân tích các số là bội của 10
Chẳng hạn khi phân tích số 3200 ta viết
3200 = 32.100 cho ta 32 = 25 và 100 = 22.52
Vậy 3200 = 27.52
Đúng 0
Bình luận (0)
| Trong các hỗn số sau, hỗn số nào lớn nhất? 2 3 10 ; 2 7 20 ; 3 1 200 ; 2 7 10 | |
\(3\dfrac{1}{200}\) lớn nhất
Đúng 0
Bình luận (0)
\(2\dfrac{3}{10};2\dfrac{7}{20};3\dfrac{1}{200};2\dfrac{7}{10}\)
\(=>\dfrac{23}{10};\dfrac{47}{20};\dfrac{601}{200};\dfrac{27}{10}\)
\(=>\dfrac{460}{200};\dfrac{470}{200};\dfrac{601}{200};\dfrac{540}{200}\)
\(=>\dfrac{601}{200}\) là lớn nhất
\(=>3\dfrac{1}{200}\) là lớn nhất
Đúng 0
Bình luận (1)

























