Bài 3:Tính góc hình thoi có cạnh bằng 4cm. Khoảng cách từ giao điểm hai đường chéo đến cạnh là 1cm

Những câu hỏi liên quan
Một hình thoi có góc nhọn bằng 30 độ. Khoảng cách từ giao điểm hai đường chéo đến các cạnh bằng h. Tính độ dài các cạnh
Cho hình chóp \(S.ABCD\), đáy \(ABCD\) là hình thoi cạnh \(a\) có \(O\) là giao điểm của hai đường chéo, \(\widehat {ABC} = {60^ \circ },SO \bot \left( {ABCD} \right),SO = a\sqrt 3 \). Tính khoảng cách từ \(O\) đến mặt phẳng \(\left( {SCD} \right)\).

Kẻ \(OI \bot C{\rm{D}}\left( {I \in C{\rm{D}}} \right),OH \bot SI\left( {H \in SI} \right)\).
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}SO \bot \left( {ABCD} \right) \Rightarrow SO \bot C{\rm{D}}\\OI \bot C{\rm{D}}\end{array} \right\} \Rightarrow C{\rm{D}} \bot \left( {SOI} \right)\\\left. \begin{array}{l} \Rightarrow C{\rm{D}} \bot OH\\OH \bot SI\end{array} \right\} \Rightarrow OH \bot \left( {SC{\rm{D}}} \right)\\ \Rightarrow d\left( {O,\left( {SC{\rm{D}}} \right)} \right) = OH\end{array}\)
\(\Delta ABC\) đều \( \Rightarrow AC = a \Rightarrow OC = \frac{1}{2}AC = \frac{a}{2}\)
\(\Delta ABD\) có \(\widehat {BA{\rm{D}}} = {120^ \circ } \Rightarrow B{\rm{D}} = \sqrt {A{B^2} + A{{\rm{D}}^2} - 2{\rm{A}}B.A{\rm{D}}} = a\sqrt 3 \Rightarrow OD = \frac{1}{2}B{\rm{D}} = \frac{{a\sqrt 3 }}{2}\)
\(\Delta OCD\) vuông tại \(O\) có đường cao \(OI\)
\( \Rightarrow OI = \frac{{OC.O{\rm{D}}}}{{C{\rm{D}}}} = \frac{{a\sqrt 3 }}{4}\)
\(SO \bot \left( {ABCD} \right) \Rightarrow SO \bot OI \Rightarrow \Delta SOI\) vuông tại \(O\) có đường cao \(OH\)
\( \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {51} }}{{17}}\)
Vậy \(d\left( {O,\left( {SCD} \right)} \right) = OH = \frac{{a\sqrt {51} }}{{17}}\).
Đúng 0
Bình luận (0)
Cho hình chữ nhật có chu vi= 40cm. Biết khoảng cách từ giao điểm 2 đường chéo đến cạnh nhỏ lớn hơn khoảng cách từ giao điểm 2 đường chéo đến cạnh lớn là 2 cm. Tính diện tích hình chữ nhật
Diện tích của một hình thoi là 540dm2. Một trong những đường chéo của nó bằng 4,5dm. Tính khoảng cách giao điểm của các đường chéo đến các cạnh.
Hình bình hành ABCD có cạnh AB=8cm, khoảng cách từ giao điểm O hai đường chéo AC và BD đến AB,
BC lần lượt bằng 3cm; 4cm.
a) Tính diện tích hình bình hành.
b) Tính độ dài cạnh BC.
Giúp mình với:
Khoảng cách giữa hai chân đường vuông góc hạ từ một đỉnh của hình thoi xuống hai cạnh của nó bằng nửa độ dài đường chéo của hình thoi. Tính các góc của hình thoi (nhớ xét cả hai trường hợp khoảng cách bằng 2 đường chéo nhé). Thanks các bạn nhiều
k/c = 1/2 dg chéo => k/c do la dg trung bình nên cạnh ben = dg cheo còn lai
tu do cac góc cua hình thoi la 60 va 120
bn vẽ hình ra la thay liền
Đúng 0
Bình luận (0)
Giúp mình với:
Khoảng cách giữa hai chân đường vuông góc hạ từ một đỉnh của hình thoi xuống hai cạnh của nó bằng nửa độ dài đường chéo của hình thoi. Tính các góc của hình thoi (nhớ xét cả hai trường hợp khoảng cách bằng 2 đường chéo nhé). Thanks các bạn nhiều
Khoảng cách giữa hai chân đường vuông góc kẻ từ 1 đỉnh hình thoi xuống hai cạnh bằng \(\frac{1}{2}\) độ dài hai đường chéo của hình thoi.
Tính các góc của hình thoi.
Ta có hình vẽ :
Xét hình thoi ABCD, E và F là chân đường vuông góc kẻ từ đỉnh A đến các cạnh BC, CD. Xét hai trường hợp :
a) Trường hợp EF = \(\frac{1}{2}\) BD
\(\Delta AEC\)= \(\Delta AFC\) (cạnh huyền và góc nhọn) nên CE = CF.
Tam giác cân CEF có CA là đường phân giác của góc C nên CA
Rồi tới bạn làm nốt
Đúng 0
Bình luận (0)
Cho hình bình hành có diện tích 48 c m 2 . Khoảng cách từ giao điểm hai đường chéo đến các cạnh của nó bằng 3cm và 4 cm. Tính chu vi của hình bình hành đó.
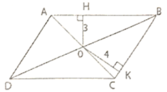
Ta có: SABCD = 2.0H.AB = 2.3.AB = 6AB
Mà SABCD = 48cm2
Suy ra 6AB = 48 => AB = 8(cm)
Mặt khác: 2OK.BC = SABCD => 2.4.BC = 48 => BC = 6(cm)
Chu vi hình bình hành ABCD là (8 + 6).2 = 28 (cm)
Đúng 0
Bình luận (0)



















