Tập nghiệm của phương trình:
I x-1 I= x+1 có số phần tử là bao nhiêu
Những câu hỏi liên quan
Phương trình
2
-
f
(
x
)
f
(
x
)
có tập nghiệm
T
1
20
;
18
;
3
. Phương trình
2
g...
Đọc tiếp
Phương trình 2 - f ( x ) = f ( x ) có tập nghiệm T 1 = 20 ; 18 ; 3 . Phương trình 2 g ( x ) - 1 + 3 g ( x ) - 2 3 = 2 g ( x ) có tập nghiệm T 2 = 0 ; 3 ; 15 ; 19 . Hỏi tập nghiệm của phương trình f ( x ) g ( x ) + 1 = f ( x ) + g ( x ) có bao nhiêu phần tử?
A. 4
B. 3
C. 11
D. 6
. Từ phương trình sau, tìm giá trị của tham số để phương trình:
i) Có nghiệm duy nhất
ii) Vô nghiệm
iii) Nghiệm đúng với mọi x ϵ R
iv) Có nghiệm.
(mx + 2)(x + 1) = (mx + m2 )x
Cho hệ phương trình
2
x
−
y
−
2
y
+
x
2
y
2...
Đọc tiếp
Cho hệ phương trình 2 x − y − 2 y + x = 2 y 2 x + 1 = m + 2 2 .2 y . 1 − y 2 ( 1 ) , m là tham số. Gọi S là tập các giá trị nguyên để hệ (1) có một nghiệm duy nhất. Tập S có bao nhiêu phần tử?
A. 0
B. 1
C. 3
D. 2
Chọn B.
Phương pháp:
+ Biến đổi phương trình thứ nhất của hệ để đưa về dạng
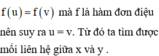
+ Thay vào phương trình thứ hai ta được phương trình ẩn y. Lập luận phương trình này có nghiệm duy nhất
thì hệ ban đầu sẽ có nghiệm duy nhất.
+ Sử dụng bất đẳng thức Cô-si để thử lại m.
Cách giải:
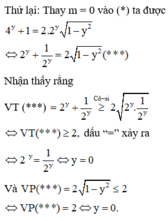
Vậy phương trình (***) có nghiệm duy nhất y = 0.
Kết luận : Với m = 0 thì hệ đã cho có nghiệm duy nhất nên tập S có một phần tử.
Chú ý :
Các em có thể làm bước thử lại như sau :
Thay m = 0 vào (*) ta được
Đúng 0
Bình luận (0)
Cho hàm số y f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên.Tập hợp nghiệm của phương trình
f
f
x
+
1
0
có bao nhiêu phần tử? A. 7 B. 6 C. 9 D. 4
Đọc tiếp
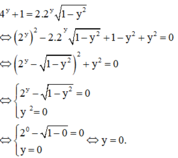
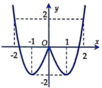
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
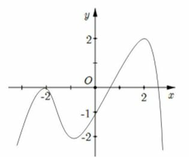
Tập hợp nghiệm của phương trình f f x + 1 = 0 có bao nhiêu phần tử?
A. 7
B. 6
C. 9
D. 4
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x.2x x(x - m +1) + m(2x - 1) có hai phần tử.Tìm số phần tử của A. A. 1 B. Vô số C. 3 D. 2
Đọc tiếp
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x.2x = x(x - m +1) + m(2x - 1) có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có
Giải (1) , đặt f(x) = 2x - x - 1. Xét hàm số f(x) = 2x - x - 1trên R, có f’(x) = 2x.ln2 - 1
Phương trình
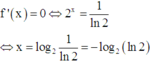
=> f(x) = 0 có nhiều nhất 2 nghiệm mà f(0) = f(1) => f(x) = 0 <=> x = 0 hoặc x = 1
Để phương trình đã cho có hai nghiệm phân biệt <=> (2) có 1 nghiệm hoặc 0
Vậy m = {0 ;1} là hai giá trị cần tìm.
Đúng 0
Bình luận (0)
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình
x
.2
x
x
x
−
m
+
1
+
m
2
x
−
1
có hai phần tử. Tìm số phần tử của A. A. 1 B. Vô số C. 3 D. 2
Đọc tiếp
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình
x
.2
x
x
x
−
m
+
1
+
m
2
x
−
1
có hai phần tử. Tìm số phần tử của A. A. 1 B. 2 C. 3 D. Vô số
Đọc tiếp
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x .2 x = x x − m + 1 + m 2 x − 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình
x
.
2
x
x
x
-
m
+
1
+
m
2
x
-
1
có hai phần tử. Tìm số phần tử của A. A. 1 B. 2 C. 3 D. Vô số
Đọc tiếp
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử. Tìm số phần tử của A.
A. 1
B. 2
C. 3
D. Vô số
Đáp án B.
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x - m 2 x = x 2 - ( m - 1 ) x - m
⇔ x - m 2 x = ( x - m ) ( x + 1 ) ⇔ x - m 2 x - x - 1 = 0 ⇔ x = m 2 x = x + 1
Giải phương trình 2 x = x + 1 .
Nhìn vào màn hình ta thấy phương trình 2 x = x + 1 có hai nghiệm phân biệt là x = 0 ; x = 1 . Do vậy để tập nghiệm của phương trình đã cho có đúng hai phần tử thì m ∈ 0 ; 1 . Vậy có 2 giá trị của m thỏa mãn, ta chọn B.
Đúng 0
Bình luận (0)
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình
x
.
2
x
x
x
-
m
+
1
+
m
2
x
-
1
có hai phần tử.Tìm số phần tử của A. A. 1 B. Vô số C. 3 D. 2
Đọc tiếp
Gọi A là tập tất cả các giá trị thực của tham số m sao cho tập nghiệm của phương trình x . 2 x = x x - m + 1 + m 2 x - 1 có hai phần tử.Tìm số phần tử của A.
A. 1
B. Vô số
C. 3
D. 2
Đáp án D
Ta có x . 2 x = x x - m + 1 + m 2 x - 1 ⇔ x . 2 x = x 2 - m x + x + m . 2 x - m
⇔ 2 x x - m = x + 1 x - m ⇔ 2 x - x - 1 x - m = 0 ⇔ [ 2 x - x - 1 = 0 ( 1 ) x - m = 0 ( 2 )
Giải (1) , đặt f x = 2 x - x - 1 . Xét hàm số f x = 2 x - x - 1 trên ℝ , có f ' x = 2 x . ln 2 - 1
Phương trình f ' x = 0 ⇔ 2 x = 1 ln 2 ⇔ x = log 2 1 ln 2 = - log 2 ln 2
⇒ f x = 0 có nhiều nhất 2 nghiệm mà f 0 = f 1 ⇒ f x = 0 ⇔ [ x = 0 x = 1
Để phương trình đã cho có hai nghiệm phân biệt ⇔ 2 có 1 nghiệm hoặc 0
Vậy m = {0;1} là hai giá trị cần tìm.
Đúng 0
Bình luận (0)