BÀI 3.Cho tam giácABCđều cạnha. Tính bán kính đường tròn đi qua ba điểmA,B,C.
BÀI 5.Cho hai điểmA,Bphân biệt. Hãy vẽ ba đường tròn đi qua hai điểmA,B.Tâm của ba đường tròn này nằm trên đường thẳng nào?
Tâm của ba đường tròn này sẽ nằm trên đường trung trực của AB
2. Cho tam giác ABC vẽ cung tròn tâm A bán kính bằng BC, vẽ cung tròn tâm C bán kính bằng BA, chúng cắt nhau ở ( D và B nằm khác phía đối với AC) CMR:AD//BC
3. Cho đường thẳng xy, các điểm A nằm ngoài xy. Dựa vào bài 34, hãy nêu cách vẽ đường thẳng đi qua A và // với BC
Cho tam giác ABC, vuông tại A đường cao AH. Biết AH = 2 căn 3, góc BAH = 60 độ. Tính bán kính đường tròn đi qua ba đỉnh của tam giác ABC
Xét \(\Delta\) vuông tại H \(ABH\) có :
\(tan\widehat{BAH}=tan60^o=\dfrac{BH}{AH}\Rightarrow BH=AH.tan60^o=2\sqrt[]{3}.\sqrt[]{3}=6\)
Xét \(\Delta\) vuông tại H \(ACH\) có :
\(\widehat{HAC}=90^o-\widehat{BAH}=90^o-60^o=30^o\)
\(tan\widehat{HAC}=tan30^o=\dfrac{CH}{AH}\Rightarrow CH=AH.tan30^o=2\sqrt[]{3}.\dfrac{1}{\sqrt[]{3}}=2\)
Tâm đường tròn ngoại tiếp tam giác vuông ABC là trung điểm BC
\(\Rightarrow\) Bán kính đường tròn này là :
\(R=\dfrac{BC}{2}=\dfrac{BH+CH}{2}=\dfrac{6+2}{2}=4\)
Bài 1 : Cho đường tròn ( O ; R ) đường kính AB = 5 cm và C là một điểm thuộc đường tròn sao cho AC = 3 cm.
a) Tam giác ABC là tam giác j? Vì sao? Tính R & Sin góc CAB
b) Đường thẳng qua C vuông gó với AB tại H, cắt đường tròn ( O ) tại D. Tính CD & chứng minhrawngf AB là tiếp tuyến của đương tròn (C ; CH )
Bài 2 : Cho đường tròn tâm I, bán kính IA = a cm, điểm M nằm bên ngoài đườn tròn và cách I là 7 cm, đường thảng đi qua M & tiếp xúc với đường tròn tại B. Tính MB
Bài 3 : Cho đường tròn tâm O, bán kính 6 cm, một điểm A cách O một khoảng là 10 cm. Kẻ tiếp tuyến AB với đường tròn (B là tiếp điểm). Tính AB
Cho tam giác đều ABC. Gọi O là tâm của đường tròn đi qua đỉnh A, B, C.
Tính số đo các góc ở tâm tạo bởi hai trong ba bán kính OA, OB, OC.
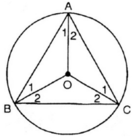
Vì tam giác ABC là tam giác đều nên 
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
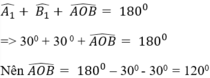
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)
Bài 10:Cho ABC có a = 8, b =10, c =13 a. ABC có góc tù hay không ? Tính bán kính đường tròn ngoại tiếp ABC. b. Tính diện tích ABC
Bài 11:Cho tam giác ABC có: a = 6, b = 7, c = 5. a) Tính S ,h ,R,r ABC a b) Tính bán kính đường tròn đi qua A, C và trung điểm M của cạnh AB.
Bài 12:Cho tam giác ABC có: AB = 6, BC = 7, AC = 8. M trên cạnh AB sao cho MA = 2 MB. a) Tính các góc của tam giác ABC. b) Tính S ,h ,R ABC a , r. c) Tính bán kính đường tròn ngoại tiếp ∆MBC.
Bài 13:Cho ABC có 0 0 A B b = = = 60 , 45 , 2 tính độ dài cạnh a, c, bán kính đường tròn ngoại tiếp và diện tích tam giác ABC
Bài 14:Cho ABC AC = 7, AB = 5 và 3 cos 5 A = . Tính BC, S, a h , R, r.
Bài 15:Cho ABC có 4, 2 m m b c = = và a =3 tính độ dài cạnh AB, AC.
Bài 16:Cho ABC có AB = 3, AC = 4 và diện tích S = 3 3 . Tính cạnh BC
Bài 17:Cho tam giác ABC có ˆ o A 60 = , c h 2 3 = , R = 6. a) Tính độ dài các cạnh của ∆ABC. b) Họi H là trực tâm tam giác ABC. Tính bán kính đường tròn ngoại tiếp ∆AHC.
Bài 18:a. Cho ABC biết 0 0 a B C = = = 40,6; 36 20', 73 . Tính BAC , cạnh b,c. b.Cho ABC biết a m = 42,4 ; b m = 36,6 ; 0 C = 33 10' . Tính AB, và cạnh c.
Bài 19:Tính bán kính đường tròn nội tiếp ABC biết AB = 2, AC = 3, BC = 4.
Bài 20:Cho ABC biết A B C (4 3; 1 , 0;3 , 8 3;3 − ) ( ) ( ) a. Tính các cạnh và các góc của ABC b. Tính chu vi và diện tích ABC
cho tam giác abc vuông tại a , ab = 12 , ac = 16 . Giải tam giác abc . Gọi am là đường trung tuyến . Tính bán kính đường tròn đi qua 3 điểm a,b,c
ΔABC vuông tại A
=>AB^2+AC^2=BC^2
=>BC^2=12^2+16^2=400
=>BC=20
Xét ΔABC vuông tại A có sin C=AB/BC=3/5
nên góc C\(\simeq\)37 độ
=>góc B=53 độ
ΔABC vuông tại A
=>A,B,C cùng nằm trên đường tròn đường kính BC
=>R=BC/2=20/2=10
Bài 1:
a/ Cho hình vuông ABCD có cạnh 5cm. Chứng minh rằng: A, B, C, D cùng nằm trên một đường tròn, tính bán kính.
b/ Cho hình chữ nhật ABDE có AB = 8, BD = 6. Chứng minh rằng: A, B, D, E cùng nằm trên một đường tròn, tính bán kính.
Bài 2: Cho tam giác ABC, vẽ đường tròn tâm O đường kính BC. (O) cắt AB, AC lần lượt tại D và E, BE giao CD tại K.
a/ CMR: CD ^ AB, BE ^ AC.
b/ CMR: AK ^ BC.
Bài 3: Cho tam giác ABC vuông ở B, AB = 8cm, BC = 6cm. Gọi D là điểm đối xứng của điểm B qua AC.
a. CMR: 4 điểm A, B, C, D cùng thuộc một đường tròn. Tính bán kính của đường tròn đó.
b. Vẽ đường kính BE của đường tròn ngoại tiếp tam giác ABC. Chứng minh tứ giác ACDE là hinh thang cân.
Bài 1. Cho tam giác ABC nội tiếp đường tròn (O), đường kính AB. Tính số đo các góc còn
lại của tam giác ABC nếu biết Ab = 40◦
Bài 3. Cho đường tròn (O;R), các điểm A,B thuộc (O) sao choAOB = 90◦
.
(a) Tính độ dài AB theo R.
(b) Gọi H là trung điểm AB. Chứng minh OH ⊥ AB.
Bài 4. Cho hình vuông ABCD có AB = a\(\sqrt{2}\)
(a) Chứng minh bốn điểm A,B,C,D cùng thuộc một đường tròn.
(b) Tính bán kính của đường tròn đi qua A,B,C,D theo a.