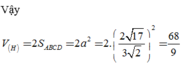cho tứ giác ABCD với diện tích S; O là điểm nằm trong tứ giác. Cmr OA2+OB2+OC2+OD2≥2S

Những câu hỏi liên quan
Cho tứ giác ABCD có diện tích S. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA
a, Tứ giác EFGH là hình gì? Vì sao?
b, Tính diện tích tứ giác EFGH theo S
a, Ta có: AE=EB , AH=HD
⇒ EH là đg TB của △ABD ⇒ EH//BD , EH=\(\dfrac{BD}{2}\)
C/m tương tự ta có: FG là đg TB của △BDC ⇒ FG//BD , FG=\(\dfrac{BD}{2}\)
⇒ EH//FG , EH=FG ⇒ tứ giác EFGH là hbh
b, SEFGH = S - (SAEH +
SEBF + SFCG + SHDG)
+
Đúng 2
Bình luận (0)
cho tứ giác ABCD nối A với C trên AC lấy E sao cho CE = 1/3 AC. Nối E với B và D biết diện tích tứ giác ABED là 45 cm2. tính diện tích tứ giác ABCD
Cho hình bình hành ABCD có diện tích S. Trên cạnh BC lấy hai điểm M, N sao cho \(BM=MN=NC=\dfrac{1}{3}BC\)
a) Tính diện tích của tứ giác ABMD theo S
b) Từ điểm N kẻ NT song song với AB (T thuộc AC). Tính diện tích của tứ giác ABNT theo S
a) dt(ABMD) = dt(ABCD) - dt(CMD)
Mà dt(CMD) = 1/2 MC.h = 1/2 . 2/3 . BC .h = 1/3 dt(ABCD) = 1/3.S
(với h là đường cao hạ từ A xuống BC của hình bình hành ABCD)
Suy ra dt(ABMD) = S - 1/3 S = 2/3. S
b) dt(ABNT) = BN.h = 2/3 BC . h = 2/3 . S
Đúng 0
Bình luận (0)
Cho tứ giác ABCD có điểm O nằm trong tứ giác ABCD. Gọi S là diện tích của tứ giác ABCD
CMR: \(OA^2+OB^2+OC^2+OD^2\ge2S\)
Hạ CH vuông góc với OB tại H. Theo quan hệ đường xiên hình chiếu:
\(CH\le OC\Leftrightarrow CH.OB\le OC.OB\Leftrightarrow2.S_{BOC}\le OC.OB\)(Do \(S_{BOC}=\frac{CH.OB}{2}\))
Áp dụng BĐT Cauchy, ta có: \(OC.OB\le\frac{OC^2+OB^2}{2}\)
\(\Rightarrow2.S_{BOC}\le\frac{OC^2+OB^2}{2}\left(1\right)\). Chứng minh tương tự ta được:
\(2.S_{AOB}\le\frac{OA^2+OB^2}{2}\left(2\right);2.S_{DOC}\le\frac{OD^2+OC^2}{2}\left(3\right);2.S_{AOD}\le\frac{OA^2+OD^2}{2}\left(4\right)\)
Cộng (1); (2); (3) và (4) theo vế:
\(2.\left(S_{BOC}+S_{AOB}+S_{DOC}+S_{AOD}\right)\le\frac{2.\left(OA^2+OB^2+OC^2+OD^2\right)}{2}\)
\(\Rightarrow2S\le OA^2+OB^2+OC^2+OD^2\)=> ĐPCM.
Đúng 0
Bình luận (0)
\(2.S_{BOC}\le OC.OB\). Dấu "=" xảy ra <=> OC vuông góc với OB
\(OC.OB\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> OC=OB
Suy ra \(2.S_{BOC}\le\frac{OC^2+OB^2}{2}\). Dấu "=" xảy ra <=> \(\Delta\)BOC vuông cân tại O
Tương tự với các tam giác AOB; AOD; DOC.
Vậy dấu "=" xảy ra <=> Tứ giác ABCD là hình vuông và O là tâm của hình vuông này.
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi K,L,M,N lần lượt là trung điểm của DC, DA, AB, BC. Gọi giao điểm của AK với BL, DN lần lượt là P và S. CM cắt BL, DN lần lượt tại Q và R
a)Xác định diện tích tứ giác PQRS nếu biết diện tích tứ giác ABCD, AMQP, CKSR tương ứng là So,S1,S2
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
2
+
z
−
2
2
9
ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y 2 + z − 2 2 = 9 ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác ABCD). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là giao tuyến của mặt cầu (S) và mặt phẳng P : 2 x + 2 y − z − 8 = 0 . Tính thể tích khối bát diện (H)
A. V H = 34 9 .
B. V H = 665 81 .
C. V H = 68 9 .
D. V H = 1330 81 .
Đáp án C
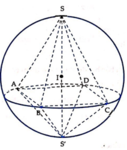
Mặt cầu (S) có tâm I 1 ; 0 ; 2 , bán kính R=3. Nhận xét thấy S, I, S’ thẳng hàng và S S ' ⊥ A B C D . Khi đó S S ' = 2 R = 6 . Ta có:
V H = V S . A B C D + V S ' . A B C D = 1 3 d S ; A B C D . S A B C D + 1 3 d S ' ; A B C D . S A B C D
= 1 3 d S ; A B C D + d S ' ; A B C D . S A B C D = 1 3 S S ' . S A B C D = 2 S A B C D
Từ giả thiết suy ra ABCD là hình vuông, gọi a là cạnh hình vuông đó.
Mặt phẳng (P) cắt mặt cầu (S) theo giao tuyến là một đường tròn có bán kính bằng r và ngoại tiếp hình vuông ABCD.
Suy ra 2 r = A C = a 2 ⇒ r = a 2 2 . Từ d I ; P 2 + r 2 = R 2 .
⇔ r = R 2 − d I ; P 2 = 3 2 − 8 3 2 = 17 3 = a 2 2 ⇔ a = 2 17 3 2
Vậy V H = 2 S A B C D = 2 a 2 = 2. 2 17 3 2 2 = 68 9 .
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu
S
:
x
−
1
2
+
y
2
+
z
−
2
2
9
ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu S : x − 1 2 + y 2 + z − 2 2 = 9 ngoại tiếp khối bát diện (H) được ghép từ hai khối chóp tứ giác đều S.ABCD và S’.ABCD (đều có đáy là tứ giác ABCD). Biết rằng đường tròn ngoại tiếp của tứ giác ABCD là giao tuyến của mặt cầu (S) và mặt phẳng P : 2 x + 2 y − z − 8 = 0 . Tính thể tích khối bát diện (H)
A. V H = 34 9 .
B. V H = 665 81 .
C. V H = 68 9 .
D. V H = 1330 81 .
cho tứ giác ABCD gọi I là giao điểm 2 đường chéo. đặt diện tích tam giác AIB là S1 ; diện tích của tam giác CID là S2 ; diện tích của tứ giác ABCD là S.
C/M: \(\sqrt{S_1}+\sqrt{S_2}\le\sqrt{S}\)
Theo mình nghĩ là đề sai
\(s_1+s_2+2\sqrt{s_1s_2}=s\)mà \(s_1+s_2=s-s_3-s_4\)
Thay vào ta được \(2\sqrt{s_1s_2}=s_3+s_4\)
Dùng cô si ta được \(2\sqrt{s_1s_2}\ge2\sqrt{s_3s_4}\)
ta ko thể chứng minh được điều này vì ko có tứ giác được xác định rõ ràng
Đúng 0
Bình luận (0)
Lập luận của bạn OX sai.
Ta có thể giải như sau: Gọi \(S_3,S_4\) tương ứng là diện tích tam giác \(AID,BIC\). Khi đó \(\frac{S_1}{S_3}=\frac{IB}{ID}=\frac{S_4}{S_2}\) (hai tam giác chung đường cao thì tỉ số diện tích bằng tỉ số hai đáy). Do đó \(S_1S_2=S_3S_4\). Ta có
\(S=S_1+S_2+S_3+S_4\ge S_1+S_2+2\sqrt{S_3S_4}=S_1+S_2+2\sqrt{S_1S_2}=\left(\sqrt{S_1}+\sqrt{S_2}\right)^2.\)
Từ đây ta suy ra \(\sqrt{S}\ge\sqrt{S_1}+\sqrt{S_2}.\)
Đúng 0
Bình luận (0)
Cho tứ giác ABCD trên ab lấy hai điểm M và N sao cho AM = MN = NP trên cạnh CD lấy Hai điểm P và Q sao cho C P = BP = QD Hãy so sánh diện tích tứ giác MNPQ với diện tích tứ giác ABCD
cho tứ giác ABCD có AB=10cm, AC=6cm, AB vuông góc với BC. Tính diện tích tứ giác ABCD?
Diện tích tứ giác ABCD là: 10 x 6=60(cm)
Đáp số: 60 cm
Ai k mk mk k cho
3 cái luôn
Đúng 0
Bình luận (0)