GIÚP MÌNH BÀI NÀY VỚIII
MÌNH CẦN GẤP Ạ
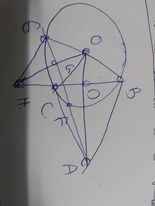
Cho điểm A nằm ngoài đường tròn ( O;R ). Vẽ 2 tiếp tuyến AM, AN với đường tròn ( M,N là tiếp điểm ) gọi H là chân đường vuông góc kẻ từ M đến đường kính ND
a) CM : MH // AN
b) Tính MN, MH biết R = 2,5cm, MD = 4cm.