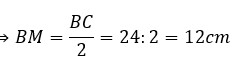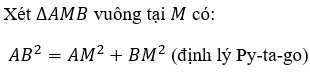tính diện tích tam giác ABC biết AB = 3 cm, AC = 5 cm, trung tuyến AM = 2 cm.

Những câu hỏi liên quan
Cho tam giác ABC, trung tuyến AM:
a) Cm diện tích tam giác AMB = diện tích tam giác AMC
b) Biết AB = 16 cm, AC = 12 cm, BC = 20 cm. Gọi N là trug điểm cạnh AC. Tính diện tích tam giác MBN.
Cho tam giác ABC, AB= 3cm , AC= 5cm, trung tuyến AM = 2 cm. Tính diện tích tam giác ABC.
diện tích tam giác là 3.5=15(cm )thế nha bạn dễ ọt yk
d
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Xét tam giác ABH vuông tại H, ta có:
\(AB^2=AH^2+BH^2\)\(=3^2+4^2=25\)
\(\Rightarrow AB=5\left(cm\right)\)
Xét tam giác ABC vuông tại A, theo hệ thức lượng ta có:
\(AH^2=AB\cdot AC\Rightarrow AC=\dfrac{AH^2}{AB}=\dfrac{3^2}{5}=1,8\left(cm\right)\)
Do đó:\(BC=\sqrt{AB^2+AC^2}=\sqrt{5^2+1,8^2}\simeq5,3\left(cm\right)\)
AM là đường trung tuyến trong tam giác vuông ABC
=> AM=\(\dfrac{1}{2}\) BC= 2,65 \(\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A có trung tuyến AM , lấy O là trung điểm AM . Tia BO cắt AC tại D , tia CO cắt AB tại E . Biết diện tích của tam giác ADE = 5 cm2. Vậy diện tích tam giác ABC là ?
Câu 1. Tính: Cho tam giác ABC vuông tại A có AB = 9 cm BC = 15 cm . Đường cao AH, trung tuyến AM. Tỉnh AC, AH, BH, AM và diện tích tam giác AHM
Vì AM là trung tuyến ứng với cạnh huyền BC nên \(AM=\dfrac{1}{2}BC=7,5\left(cm\right)\)
Áp dụng PTG: \(AC=\sqrt{BC^2-AB^2}=12\left(cm\right)\)
Áp dụng HTL: \(\left\{{}\begin{matrix}AH=\dfrac{AB\cdot AC}{BC}=7,2\left(cm\right)\\BH=\dfrac{AB^2}{BC}=5,4\left(cm\right)\end{matrix}\right.\)
Áp dụng PTG: \(HM=\sqrt{AM^2-AH^2}=2,1\left(cm\right)\)
Vậy \(S_{AHM}=\dfrac{1}{2}HM\cdot AH=\dfrac{1}{2}\cdot2,1\cdot7,2=7,56\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC vuông tại A có đường cao AH và đường trung tuyến AM .Biết AH = 3cm, HB = 4 cm. Hãy tính AB AC AM , và diện tích tam giác ABC .
Tính diện tích tam giác ABC biết AB = 3 cm , AC = 5 cm , trung tuyến AM = 2 cm
Gọi N là trung điểm của \(AC.\)
=> \(AN=CN=\frac{1}{2}AC\) (tính chất trung điểm).
=> \(AN=CN=\frac{1}{2}.5=\frac{5}{2}=2,5\left(cm\right).\)
+ Xét \(\Delta ABC\) có:
\(M\) là trung điểm của \(BC\) (vì \(AM\) là đường trung tuyến).
\(N\) là trung điểm của \(AC\) (do cách vẽ).
=> \(MN\) là đường trung bình của \(\Delta ABC.\)
=> \(MN=\frac{1}{2}AB\) (tính chất đường trung bình của tam giác).
=> \(MN=\frac{1}{2}.3=\frac{3}{2}=1,5\left(cm\right).\)
Ta có:
\(AM^2+MN^2=2^2+\left(1,5\right)^2\)
\(\Rightarrow AM^2+MN^2=4+2,25\)
\(\Rightarrow AM^2+MN^2=6,25cm\) (1).
Có:
\(AN^2=\left(2,5\right)^2\)
\(\Rightarrow AN^2=6,25cm\) (2).
Từ (1) và (2) => \(AM^2+MN^2=AN^2\left(=6,25cm\right).\)
=> \(\Delta AMN\) vuông tại \(M\) (định lí Py - ta - go đảo).
+ Diện tích \(\Delta AMN\) là:
\(S_{AMN}=\frac{1}{2}AM.MN=\frac{1}{2}.2.1,5=1,5\left(cm^2\right).\)
+ Diện tích \(\Delta ABC\) là:
\(S_{ABC}=4S_{AMN}=4.1,5=6\left(cm^2\right).\)
Vậy \(S_{ABC}=6\left(cm^2\right).\)
Chúc bạn học tốt!
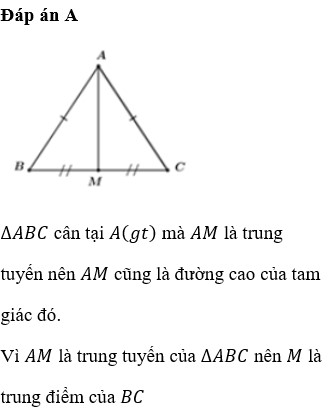
Cho tam giác ABC cân tại A, trung tuyến AM. Biết BC=24 cm, AM=5 cm. Tính độ dài các cạnh AB, AC
A. AB=AC=13 cm
B. AB=AC=14 cm
C. AB=AC=15 cm
D. AB=AC=16 cm
Cho tam giác ABC, có độ dài 3 cạnh là AB = 4, 5 cm ; BC = 7, 5 cm ; AC = 6 cm và đường trung tuyến AM. Tính trung tuyến AM.
\(\Delta ABC\)có : AB2 + AC2 = (4,5)2 + 62 = 56,25 = (7,5)2 = BC2 nên\(\Delta ABC\)vuông tại A
=> Trung tuyến AM bằng nửa cạnh huyền BC và bằng : 7,5 : 2 = 3,75 (cm)
Đúng 0
Bình luận (0)