Có bao nhiêu sắp 4 nam và 3 nữ ngồi dãy dãy ghế 9 chổ sao cho nam ngồi gần nhau,nữ ngồi gần nhau

Những câu hỏi liên quan
Một tổ có 9 học sinh gồm 5 nam và 4 nữ.
a) Có bao nhiêu cách xếp 9 học sinh đó vào một dãy bàn có 9 ghế sao cho các học sinh nữ luôn ngồi gần nhau.
Vì các bạn nữ luôn ngồi gần nhau nên ta coi 4 bạn nữ là x
=> Có 4! cách xếp x
số cách xếp 5 học sinh nam và x là :
6!.4! = 17280 (cách)
Đúng 0
Bình luận (0)
Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ, ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau bằng
A
.
8
35
B
.
1
35
C
.
2...
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có bốn ghế. Xếp ngẫu nhiên 8 học sinh, gồm 4 nam và 4 nữ, ngồi vào hai dãy ghế sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau bằng
A . 8 35
B . 1 35
C . 2 35
D . 4 35
Chọn B
Số phần tử của không gian mẫu là số cách sắp xếp 8 học sinh vào 8 chỗ ngồi khác nhau. Suy ra n ( Ω ) = 8!
Gọi A là biến cố xếp 8 học sinh sao cho mỗi học sinh nam đều ngồi đối diện với một học sinh nữ và không có hai học sinh cùng giới ngồi cạnh nhau. Ta đánh số các chỗ ngồi từ 1 đến 8 như sau:
Dãy 1:
| 1 |
2 |
3 |
4 |
Dãy 2:
| 8 |
7 |
6 |
5 |
Để sắp xếp các học sinh ngồi vào vị trí thỏa mãn yêu cầu bài toán ta sắp xếp như sau:
Trường hợp 1: 4 học sinh nam ngồi vào các số lẻ, 4 học sinh nữ ngồi vào các số chẵn. Trường hợp này có 4!4! cách.
Trường hợp 2: 4 học sinh nam ngồi vào các số chẵn, 4 học sinh nữ ngồi vào các số lẻ. Trường hợp này có 414! cách.
Do đó n(A) = 2.4!.4!
Vậy xác suất của biến cố A là 
Đúng 0
Bình luận (0)
Ba ông và ba bà ngồi trên một dãy ghế.
1. Tính xác suất để người cùng phái ngồi gần nhau.
2. Tính xác suất để ba bà ngồi gần nhau.
3. Tính xác suất để họ ngồi nam nữ xen kẽ nhau.
Ba ông và ba bà ngồi trên một dãy 6 ghế.
1. Tính xác suất để người cùng phái ngồi gần nhau.
2. Tính xác suất để ba bà ngồi gần nhau.
3. Tính xác suất để họ ngồi nam nữ xen kẽ nhau.
Kí hiệu tắt ông là M và bà là W. Không gian mẫu E có \(6!=720\) (phần tử).
1.
Có 2 cách xếp người cùng phái ngồi gần nhau: \(MMMWWW,WWWMMM\).
Có \(3!=6\) cách ngồi của 3 ông và có \(3!=6\) cách ngồi của 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
2.
Có 4 cách sắp xếp 3 bà ngồi gần nhau: \(MMMWWW,MMWWWM,MWWWMM,WWWMMM\).
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{4.3!.3!}{6!}=\dfrac{1}{5}\).
3.
Có 2 cách sắp xếp 3 ông và 3 bà ngồi xen kẽ nhau: \(MWMWMW,WMWMWM.\)
Có \(3!=6\) cách sắp xếp 3 ông và có \(3!=6\) cách sắp xếp 3 bà.
Vậy xác suất phải tính là \(P=\dfrac{2.3!.3!}{6!}=\dfrac{1}{10}\)
Đúng 1
Bình luận (0)
Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:
A
.
2
5
B
.
1
10
C
.
3
5
D
....
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có 3 ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng:
A . 2 5
B . 1 10
C . 3 5
D . 1 20
Chọn A.
Số phần tử của không gian mẫu là n(W =) 6!.
Gọi A là biến cố : "Các bạn học sinh nam ngồi đối diện các bạn nữ".
Chọn chỗ cho học sinh nam thứ nhất có 6 cách.
Chọn chỗ cho học sinh nam thứ 2 có 4 cách (không ngồi đối diện học sinh nam thứ nhất)
Chọn chỗ cho học sinh nam thứ 3 có 2 cách (không ngồi đối diện học sinh nam thứ nhất, thứ hai).
Xếp chỗ cho 3 học sinh nữ : 3! cách.
Theo quy tắc nhân ta có cách
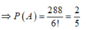
Đúng 0
Bình luận (0)
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng A.
2
5
B.
1
20
C.
3
5
D.
1
10...
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A. 2 5
B. 1 20
C. 3 5
D. 1 10
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng A.
2
5
B.
1
20
C.
3
5
D.
1
10
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A. 2 5
B. 1 20
C. 3 5
D. 1 10
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng A.
2
5
B.
1
20
C.
3
5
D.
1
10
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
A. 2 5
B. 1 20
C. 3 5
D. 1 10
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
Đọc tiếp
Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh, gồm 3 nam và 3 nữ, ngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học sinh nam đều ngồi đối diện với một học sinh nữ bằng
![]()
![]()
![]()
![]()













