Trên hình bên cho biết : AB = DC , AD = BC.
CMr: AB//DC,AD//BC
Trên hình vẽ bên cho biết
AD vuông góc vs DC, DC vuông góc với BC ,AH vuông góc với BC
AB=13cm,AC = 15 cm ,DC = 12 cm
Tính độ dài đoạn thẳng BC.
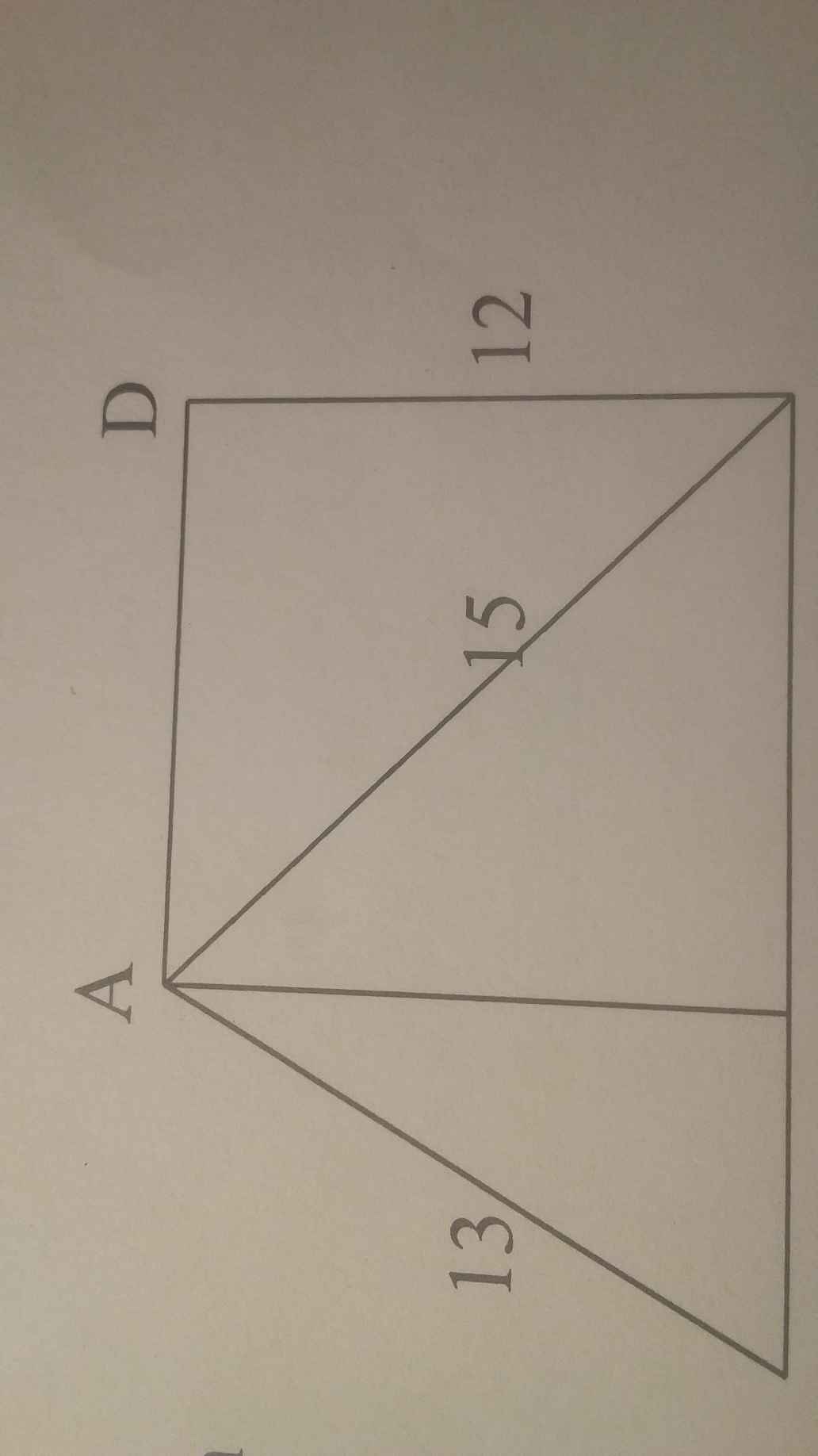
Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)
Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, ∠ ADC = 40 ° ; ∠ ABC = 90 ° (hình bên). Hãy tính:
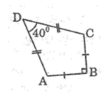
Chiều dài cạnh AD.
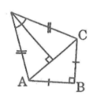
a. Nối AC và kẻ DH ⊥ AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
A C 2 = A B 2 + B C 2 = 12 2 + 12 2 = 144 + 144 = 288
Suy ra: AC = 12 2 (cm)
Ta có: ∆ ACD cân tại D
DH ⊥ AC
Áp dụng định lý Py-ta-go vào tam giác vuông OAB, ta được:
\(AB^2=OB^2+OA^2\)(1)
Áp dụng định lý Py-ta-go vào tam giác vuông ODC, ta được:
\(DC^2=OD^2+OC^2\)(2)
Từ (1) và (2) -> \(AB^2+CD^2=OA^2+OB^2+OC^2+OD^2\left(3\right)\)
Áp dụng đính lý Py-ta-go vào tam giác vuông OBC, ta được:
\(BC^2=OC^2+OB^2\left(4\right)\)
Áp dụng định lý Py-ta-go vào tam giác vuông OAD, ta được:
\(AD^2=OA^2+OD^2\left(5\right)\)
Từ (4) và (5) ta có: \(BC^2+AD^2=OB^2+OC^2+OA^2+OD^2\left(6\right)\)
Từ (3) và (6) suy ra \(AB^2+DC^2=BC^2+AC^2\)
Mỏi tay vc:vv
Cho biết AB=DC, AD=BC. Chứng minh AB // DC; AD // BC
Cho hình thang cân ABCD, có AB//DC và AD>DC. Đường chéo BD vuông góc với cạnh bên BC, kẽ đường cao DH.
a/ CM tam giác BDC đồng dạng tam giác HBC.
b/ biết BC=15cm, DC=25cm. Tính HC Và HD.
Sửa đề: đường cao BH
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
cho hình thang ABCD ( như hình vẽ bên ) biết AB = 6cm, AD = 12cm , BC = 2/3 AD
a)tính SABCD
b)kéo dài các cạnh bên AB và DC chúng gặp nhau tại K ( như hình vẽ )tính độ dài đoạn KB
Cho hình thang ABCD có AB song song với CD. Biết AB = 60cm, CD = 90cm, đường cao AH = 30cm. Trên cạnh AD lấy điểm E sao cho DE = 1/3 AD. Kẻ EF song song với DC. F nằm trên cạnh BC. Hãy so sánh EF và DC.
a) Nối A với F 
Và D với F
Ta có:
ED=1/3 AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
Câu 6: Chọ đáp án đúng
Trong hình vẽ bên:
A. Cạnh AB song song với cạnh DC
B. Cạnh AD song song với cạnh BC
C. Cạnh AD vuông góc với cạnh DC
D. Cạnh AB vuông góc với cạnh DC
Một chiếc diều ABCD có AB = BC, AD = DC. Biết AB = 12cm, ∠ ADC = 40 ° ; ∠ ABC = 90 ° (hình bên). Hãy tính:
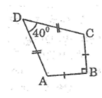
Diện tích của chiếc diều.
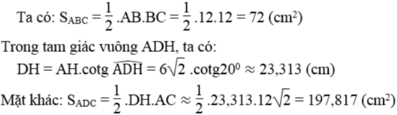
Vậy S d i ề u = S A B C + S A D C = 72 + 197 , 817 = 269 , 817 c m 2