Theo Cô si       4x+\frac{1}{4x}\ge24x+4x1​≥2  , đẳng thức xảy ra khi và chỉ khi   4x=\frac{1}{4x}=1\Leftrightarrow x=\frac{1}{4}4x=4x1​=1⇔x=41​). Do đó

                                         A\ge2-\frac{4\sqrt{x}+3}{x+1}+2016A≥2−x+14x​+3​+2016

                                        A\ge4-\frac{4\sqrt{x}+3}{x+1}+2014A≥4−x+14x​+3​+2014

                                        A\ge\frac{4x-4\sqrt{x}+1}{x+1}+2014=\frac{\left(2\sqrt{x}-1\right)^2}{x+1}+2014\ge2014A≥x+14x−4x​+1​+2014=x+1(2x​−1)2​+2014≥2014

Hơn nữa    A=2014A=2014 khi và chỉ khi \left\{{}\begin{matrix}x=\dfrac{1}{4}\\2\sqrt{x}-1=0\end{matrix}\right.{x=41​2x​−1=0​  \Leftrightarrow x=\dfrac{1}{4}⇔x=41​ .

Vậy  GTNN  =  2014

a) Vẽ đồ thị

b) Gọi y_A, y_B, y_C lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:

y_A =  . (-1,5)²  =  . 2,25 = 1,125

y_B = (-1,5)² = 2,25

y_C = 2 (-1,5)² = 2 . 2,25 = 4,5

c) Gọi y_A, y_B, y_C’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:

y_A, =  . 1,5²  =  . 2,25 = 1,125

y_B, = 1,5² = 2,25

y_C’ = 2 . 1,5² = 2 . 2,25 = 4,5

Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.

d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.

Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

1. a) Để hs trên là hs bậc nhất khi và chỉ khi a>0 --> 3+2k>0 --> k >\(\frac{-3}{2}\)

    b) Vì đths cắt trục tung tại điểm có tung độ = 5 --> x=0, y=5

       Thay y=5 và x=0 vào hs và tìm k

2. a) Tự vẽ

    b) Hệ số góc k=\(\frac{-a}{b}=\frac{-2}{4}=\frac{-1}{2}\)

    c) Phương trình hoành độ giao điểm là:\(2x+4=-x-2\)(tìm x rồi thay x vào 1 trong 2 pt --> tính y)  (x=-2; y=0)

3. Vì 3 đg thẳng đồng quy -->d1 giao d2 giao d3 tại 1 điểm (giao kí hiệu là chữ U ngược)

       Tính tọa độ giao điểm của d1 và d2 --> x=2;y=1

        Điểm (2;1) thuộc d3 --> Thay x=2 và y=1 vào d3 -->m=3

a) Vẽ đồ thị

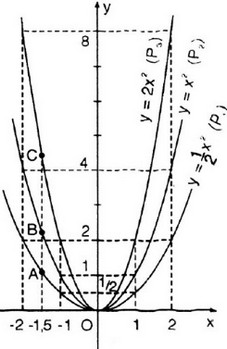
b) Gọi y_A, y_B, y_C lần lượt là tung độ các điểm A, B, C có cùng hoành độ x = -1,5. Ta có:

y_A = . (-1,5)² = . 2,25 = 1,125

y_B = (-1,5)² = 2,25

y_C = 2 (-1,5)² = 2 . 2,25 = 4,5

c) Gọi y_A, y_B, y_C’ lần lượt là tung độ các điểm A', B', C' có cùng hoành độ x = 1,5. Ta có:

y_A, = . 1,5² = . 2,25 = 1,125

y_B, = 1,5² = 2,25

y_C’ = 2 . 1,5² = 2 . 2,25 = 4,5

Kiểm tra tính đối xứng: A và A', B và B', C và C' đối xứng với nhau qua trục tung Oy.

d) Với mỗi hàm số đã cho ta đều có hệ số a > 0 nên O là điểm thấp nhất của đồ thị. Khi đó ta có x = 0.

Vậy x = 0 thì hàm số có giả trị nhỏ nhất.

Gọi `M(x;3/2x+5/2)`

Ta có:`|\vec{MA}-2\vec{MB}|`

`=|(4-x;7-3/2x-5/2)-2(2-x;1-3/2x-5/2)|`

`=|(x;3/2x+17/2)|`

`=\sqrt{x^2+(3/2x+17/2)^2}`

`=\sqrt{x^2+9/4x^2+51/2x+289/4}`

`=\sqrt{13/4x^2+51/2x+289/4}`

`=\sqrt{(\sqrt{13}/2 x+[51\sqrt{13}]/26)^2+289/13} >= [17\sqrt{13}]/13`

Dấu "`=`" xảy ra `<=>\sqrt{13}/2x+[51\sqrt{13}]/26=0<=>x=-51/13`

   `=>M(-51/13;-44/13)`

b: Tọa độ điểm A là:

\(\left\{{}\begin{matrix}y_A=0\\0.5x+2=0\end{matrix}\right.\Leftrightarrow A\left(-4;0\right)\)

Tọa độ điểm B là:

\(\left\{{}\begin{matrix}y_B=0\\5-2x_B=0\end{matrix}\right.\Leftrightarrow B\left(2.5;0\right)\)

Tọa độ điểm C là:

\(\left\{{}\begin{matrix}0.5x+2=5-2x\\y=-2x+5\end{matrix}\right.\Leftrightarrow C\left(1.2;2.6\right)\)

c: \(AB=6.5\)

\(BC=\sqrt{\left(1.2-2.5\right)^2+2.6^2}=\dfrac{13\sqrt{5}}{10}\)

\(AC=\sqrt{\left(1.2+4\right)^2+2.6^2}=\dfrac{13\sqrt{5}}{5}\)

Vì \(AC^2+BC^2=AB^2\) nên ΔABC vuông tại C

\(C=6.5+\dfrac{13\sqrt{5}}{10}+\dfrac{13\sqrt{5}}{5}=\dfrac{65+39\sqrt{5}}{10}\)

\(S=\dfrac{13\sqrt{5}}{10}\cdot\dfrac{13\sqrt{5}}{5}=16.9\)