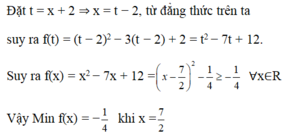Tìm giá trị nhỏ nhất của hàm số y = ( 3x^2 + x + 1) / 3x -2 với x > 2/3

Những câu hỏi liên quan
Cho đồ thị:
(
C
)
:
y
3
x
-
2
-
2
x
-
6
Tìm giá trị lớn nhất và nhỏ nhất của hàm số với -3≤ x≤ 4 A. max y 4; min y2 B. max y 2; min y -4 C.max y4; min y-2 D. max y2; min y -2
Đọc tiếp
Cho đồ thị: ( C ) : y = 3 x - 2 - 2 x - 6 Tìm giá trị lớn nhất và nhỏ nhất của hàm số với -3≤ x≤ 4
A. max y= 4; min y=2
B. max y= 2; min y= -4
C.max y=4; min y=-2
D. max y=2; min y= -2
Ta có: 
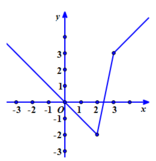
+Vẽ đường thẳng y= x với x≥3 đi qua hai điểm O(0; 0) và A(1;1) và lấy phần đường thẳng bên phải của đường thẳng x= 3.
+Vẽ đường thẳng y=5x-12 với 2≤ x≤ 3 đi qua hai điểm B(3;3) và C( 2; -2) và lấy phần đường thẳng nằm giữa của hai đường thẳng x=2; x=3.
+Vẽ đường thẳng y= -x đi qua hai điểm O và D( -1; -1) và lấy phần đường thẳng bên trái của đường thẳng x= 2
+ Dựa vào đồ thị hàm số ta có:
![]()
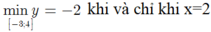
Chọn C.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị m để giá trị nhỏ nhất của hàm số:1/ ydfrac{x+m}{x-1} trên left[2;4right] bằng 3.2/ y2x^3-3x^2-m trên left[-1;1right] bằng 1.3/ yleft|x^3-3x^2+mright| trên left[0;3right] bằng 2.
Đọc tiếp
Tìm tất cả các giá trị \(m\) để giá trị nhỏ nhất của hàm số:
1/ \(y=\dfrac{x+m}{x-1}\) trên \(\left[2;4\right]\) bằng 3.
2/ \(y=2x^3-3x^2-m\) trên \(\left[-1;1\right]\) bằng 1.
3/ \(y=\left|x^3-3x^2+m\right|\) trên \(\left[0;3\right]\) bằng 2.
tìm giá trị lớn nhất và nhỏ nhất của hàm số trên [-3;1]
\(y=x^3-3x^2-1\)
ta tính
\(y'=3x^2-6x=3x\left(x-2\right)\)
giải pt y'= 0 ta có \(3x\left(x-2\right)=0\) suy ra x=0 hoặc x=2
nhìn vào bảng bt ta có giái trị lớn nhất của hàm số =3 khi x=0, hàm số đạt giá trị nhỏ nhất =-55 khi x=-3
Đúng 0
Bình luận (0)
hàm số đạt giái trị lớn nhất =-1 khi x=0, nhỏ nhất =-55 khi x=-3
Đúng 0
Bình luận (0)
TÌm tất cả các giá trị của tham số a để giá trị nhỏ nhất của hàm số y = f(x) = 4x^2-4ax +(a^2 - 3x + 2) trên đoạn [0,2] là bằng 3
cho hàm số y=3x-1. Tìm giá trị nhỏ nhất, lớn nhất của hàm số biết\(-2\le x\le3\)
Xem chi tiết
Tìm giá trị nhỏ nhất lớn nhất của hàm số y=2X^3+3x^2-12x+1 trên [-1;5]?
\(y'=6x^2+6x-12=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
\(y\left(-1\right)=14\) ; \(y\left(1\right)=-6\) ; \(y\left(5\right)=266\)
\(\Rightarrow\min\limits_{\left[-1;5\right]}y=-6\) ; \(\max\limits_{\left[-1;5\right]}y=266\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
f
(
x
)
biết rằng
f
(
x
+
2
)
x
2
−
3
x
+
2
A.
-
1
4
B.
1
4
C.
1
2
D. 0
Đọc tiếp
Tìm giá trị nhỏ nhất của hàm số f ( x ) biết rằng f ( x + 2 ) = x 2 − 3 x + 2
A. - 1 4
B. 1 4
C. 1 2
D. 0
Tính giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
\(y=x^3-3x^2-9x+35\) trên các đoạn [-4; 4] và [0;5] ;
\(y'=3x^2-6x-9=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
a. Trên [-4;4] ta có:
\(y\left(-4\right)=-41\) ; \(y\left(-1\right)=40\) ; \(y\left(3\right)=8\) ; \(y\left(4\right)=15\)
\(\Rightarrow y_{min}=-41\) ; \(y_{max}=40\)
b. Trên [0;5] ta có:
\(y\left(0\right)=35\) ; \(y\left(3\right)=8\); \(y\left(5\right)=40\)
\(\Rightarrow y_{max}=40\) ; \(y_{min}=8\)
Đúng 2
Bình luận (0)
Tìm m để 2 đường thẳng x-y=3-m và y=3x-m-3 cắt nhau tại 1 điểm B(x;y) để P=y^2-3x^2 đạt giá trị nhỏ nhất. Tìm giá trị nhỏ nhất đó.
Ta có : x - y = 3 - m
=> y = x - 3 + m (1)
Lại có y = 3x - m - 3 (2)
Từ (1) và (2) => 2y = 4x - 6
=> y = 2x - 3
Khi đó P = (2x - 3)2 - 3x2
= x2 - 12x + 9 \(=\left(x-6\right)^2-27\ge-27\)
Dấu "=" xảy ra <=> x = 6
Khi x = 6 => y = 9 => m = 6
Vậy khi m = 6 thì PMin = -27
Đúng 0
Bình luận (0)