Do \(OB=OE=R\Rightarrow\Delta OBE\) cân tại O

Mà \(OH\perp BE\) (giả thiết) \(\Rightarrow OH\) là đường cao đồng thời là trung trực của BE

Hay OA là trung trực của BE

\(\Rightarrow AB=AE\)

Xét hai tam giác OAB và OAE có: \(\left\{{}\begin{matrix}OB=OE=R\\AB=AE\left(cmt\right)\\OA\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta OAB=\Delta OAE\left(c.c.c\right)\)

\(\Rightarrow\widehat{AEO}=\widehat{ABO}=90^0\Rightarrow AE\) là tiếp tuyến của (O)

a: Xét tứ giác ABOC có 

\(\widehat{ABO}+\widehat{ACO}=180^0\)

Do đó: ABOC là tứ giác nội tiếp

c: Xét (O) có 

ΔBED nội tiếp

BD là đường kính

Do đó: ΔBED vuông tại E

Xét ΔBAD vuông tại B có BE là đường cao

nên \(AE\cdot AD=AB^2\left(1\right)\)

Xét ΔOBA vuông tại B có BH là đường cao

nên \(AH\cdot AO=AB^2\left(2\right)\)

Từ (1) và (2) suy ra \(AE\cdot AD=AH\cdot AO\)

hay \(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

Xét ΔAEH và ΔAOD có 

\(\dfrac{AE}{AO}=\dfrac{AH}{AD}\)

\(\widehat{HAE}\) chung

Do đó: ΔAEH\(\sim\)ΔAOD

Suy ra: \(\widehat{AHE}=\widehat{ADO}=\widehat{BDE}\)

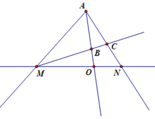
Tia MB cắt đoạn thẳng AO tại điểm B nằm giữa A và O nên tia MB nằm giữa hai tia MA, MO (hay tia MB nằm giữa hai tia MA, MN).

Vì tia MB nằm giữa hai tia MA, MN nên tia MB cắt đoạn thẳng AN tại điểm C nằm giữa hai điểm A, N.

Vậy tia MB cắt tia AN tại điểm C nằm giữa A, N. 

a: Xét tứ giác MBOC có \(\widehat{MBO}+\widehat{MCO}=90^0+90^0=180^0\)

=>MBOC là tứ giác nội tiếp

=>M,B,O,C cùng thuộc một đường tròn

b: Sửa đề: \(CH\cdot HB=OH\cdot HM\)

Xét (O) có

MB,MC là các tiếp tuyến

Do đó: MB=MC

=>M nằm trên đường trung trực của BC(1)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1) và (2) suy ra MO là đường trung trực của BC

=>MO\(\perp\)BC tại H và H là trung điểm của BC

Xét ΔOBM vuông tại B có BH là đường cao

nên \(OH\cdot HM=HB^2\)

=>\(OH\cdot HM=HB\cdot HC\)

Câu a),b) tự làm nhé , mình chỉ giúp câu c) thôi . 

OI vuông góc NP ( Do I là trung điểm của MP ) , OF vuông góc NP ( Do OF là đường trung trực của NP )
=> O,I,F thẳng hàng
Tam giác ONF vuông tại N , đường cao NI
=> ON^2 = OI.OF
Mà ON=OA
OA^2 = OH.OM
=> OH.OM=OI.OF
=> OH/OI=OF/OM
Xét tam giác OIM và tam giác OHF có
góc MOF chung
OH/OI=OF/OM
=> Tam giác OIM đồng dạng tam giác OHF
=> góc OHF=góc OIM (=90 độ )
OH vuông HF
mà OH vuông AB
=> A,B,F thẳng hàng
=> F nằm trên đường thẳng cố định AB khi đường thẳng d quay quanh M mà vẫn thỏa mãn các yêu cầu đề bài
Điều phải chứng minh

Có \(\widehat{ACP}=\dfrac{1}{2}sđ\stackrel\frown{AC}\) ( góc hợp bởi tiếp tuyến và dây cung)

Có \(\widehat{ABC}=\dfrac{1}{2}sđ\stackrel\frown{AC}\)

Suy ra \(\widehat{ACP}=\widehat{ABC}\)

Xét hai tam giác \(PBC\) và \(PCA\) có:

\(\widehat{P}\) chung

\(\widehat{PBC}=\widehat{PCA}\) 

nên \(\Delta PBC\sim\Delta PCA\) (g.g)

\(\Rightarrow\dfrac{PB}{PC}=\dfrac{PC}{PA}\Leftrightarrow PB.PA=PC^2\)

Đi nấu cơm... Mẫu hậu đang giục