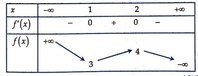
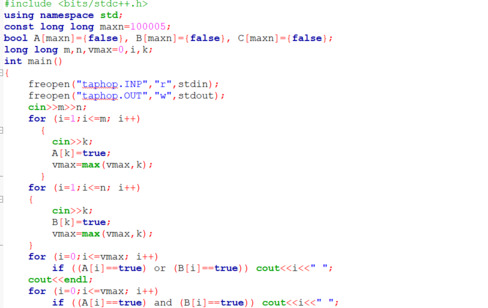
Cho tập hợp S = {a1;a2;a3;...a12} gồm 12 phần tử phân biệt. Số các tập con của S có tính chất chỉ số của mỗi phần tử trong tập con là bội của chỉ số nhỏ nhất trong tập đó là?

Những câu hỏi liên quan
Cho hàm số
y
x
3
−
6
x
2
+
9
x
−
1
và điểm
A
1
;
m
. Gọi S là tập hợp tất cả các giá trị thực của m sao cho có đúng một tiếp tuyến của đồ thị hàm số đi qua A. Biết S là hợp của một số khoảng rời nhau. Có bao nhiêu khoảng như vậy? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = x 3 − 6 x 2 + 9 x − 1 và điểm A 1 ; m . Gọi S là tập hợp tất cả các giá trị thực của m sao cho có đúng một tiếp tuyến của đồ thị hàm số đi qua A. Biết S là hợp của một số khoảng rời nhau. Có bao nhiêu khoảng như vậy?
A. 4
B. 3
C. 2
D. 1
Cho hàm số
y
x
3
-
6
x
2
+
9
x
-
1
và điểm
A
1
;
m
. Gọi S là tập hợp tất cả các giá trị thực của m sao cho có đúng một tiếp tuyến của đồ thị hàm số đi qua A. Biết S là hợp của một số khoảng rời nhau. Có bao nhiêu khoảng như vậy? A. 4 B. 3 C. 2 D. 1
Đọc tiếp
Cho hàm số y = x 3 - 6 x 2 + 9 x - 1 và điểm A 1 ; m . Gọi S là tập hợp tất cả các giá trị thực của m sao cho có đúng một tiếp tuyến của đồ thị hàm số đi qua A. Biết S là hợp của một số khoảng rời nhau. Có bao nhiêu khoảng như vậy?
A. 4
B. 3
C. 2
D. 1
Đáp án C.
Ta có y ' = 3 x 2 - 12 x + 9 .
Gọi M x 0 ; y 0 là tiếp điểm của tiếp tuyến đi qua A của đồ thị hàm số.
Lúc này tiếp tuyến có phương trình
y = 3 x o 2 - 12 x 0 + 9 x - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
Tiếp tuyến đi qua A 1 ; m ⇒ m = 3 x 0 2 - 12 x 0 + 9 1 - x 0 + x 0 3 - 6 x 0 2 + 9 x 0 - 1
⇔ m = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 (*).
Để có đúng một tiếp tuyến của đồ thị hàm số đi qua A thì phương trình (*) có duy nhất một nghiệm.
Xét hàm số f ( x ) = - 2 x 0 3 + 9 x 0 2 - 12 x 0 + 8 có bảng biến thiên
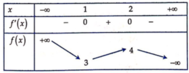
Để phương trình (*) có nghiệm duy nhất thì m > 4 m < 3 ⇔ m ∈ - ∞ ; 3 ∪ 4 ; + ∞ .
Vậy ta chọn C.
Đúng 0
Bình luận (0)
Cho tập hợp A gồm n phần tử là a1, a2, ..., an, và tập hợp B gồm m phần tử là b1, b2, ...,
bm.
Nhiệm vụ của bạn là hãy tìm số lượng của 2 tập hợp:
- Tập hợp thứ nhất là hợp của hai tập hợp A và B
- Tập hợp thứ hai là giao của hai tập hợp A và B
(lập trình pascal)
Tập hợp A{0,1,2,3,4,5,6,7}; E{
a
1
a
2
a
3
a
4
¯
/
a
1
,
a
2
,
a
3
,
a
4
...
Đọc tiếp
Tập hợp A={0,1,2,3,4,5,6,7}; E={ a 1 a 2 a 3 a 4 ¯ / a 1 , a 2 , a 3 , a 4 ∈ A , a 1 ≠ 0 }
Lấy 1 phần tử thuộc E bất kỳ. Tính xác suất để số đó chia hết cho 5
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Đáp án D
Số phần tử của tập ![]()
Để ![]() chia hết cho 5 điều kiện cần và đủ là
chia hết cho 5 điều kiện cần và đủ là ![]() hay
hay ![]()
Nếu ![]() thì lấy trong 7 chữ số 1,2,...,7
thì lấy trong 7 chữ số 1,2,...,7
Vậy có ![]() số tận cùng bằng 0
số tận cùng bằng 0
Nếu ![]() thì các số
thì các số ![]() là
là ![]() số
số
Vây xác suất để số đó chia hết cho 5 là 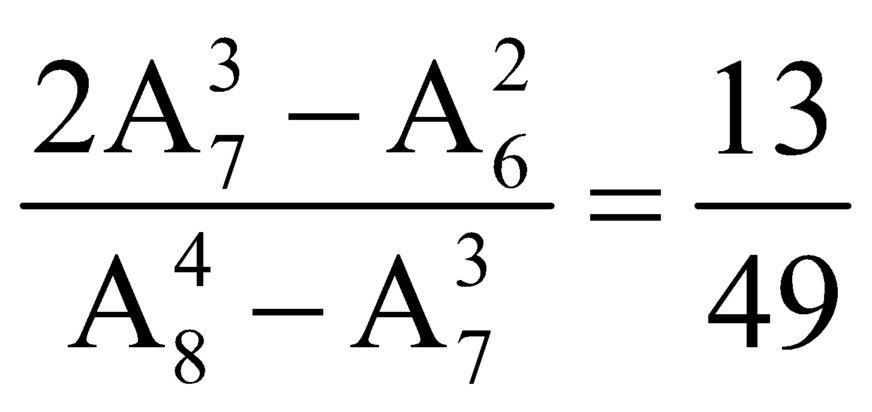
Đúng 0
Bình luận (0)
Tập hợp
A
0
;
1
;
2
;
3
;
4
;
5
;
6
;
7
,
E
a
1
a
2
a
3
a
4
/
a
1
;
a...
Đọc tiếp
Tập hợp A = 0 ; 1 ; 2 ; 3 ; 4 ; 5 ; 6 ; 7 , E = a 1 a 2 a 3 a 4 / a 1 ; a 2 ; a 3 ; a 4 ∈ A , a 1 ≠ 0 . Lấy 1 phần tử thuộc E bất kỳ. Tính xác suất để số đó chia hết cho 5
A. 5/16
B. 13/98
C. 1/4
D. 13/49
Cho hai tập hợp điểm:- Tập hợp E có n điểm
A
1
,
A
2
,
A
3
,
.
..
,
A
n
;- Tập hợp F có m điểm
B
1
,
B
2
,
B
3
,
.
..
,
B
m...
Đọc tiếp
Cho hai tập hợp điểm:
- Tập hợp E có n điểm A 1 , A 2 , A 3 , . .. , A n ;
- Tập hợp F có m điểm B 1 , B 2 , B 3 , . .. , B m ;
Có tất cả bao nhiêu đoạn thẳng có 1 đầu thuộc E và đầu kia thuộc F?
Nối A 1 ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có m đoạn thẳng A 1 B 1 , A 1 B 2 , A 1 B 3 , . .. , A 1 B m . Lần lượt nối A 1 , A 2 , A 3 , . .. , A n ∈ E với m điểm B 1 , B 2 , B 3 , . .. , B m ∈ F ta có số đoạn thẳng có một đầu thuộc E và một đầu thuộc F là m.n đoạn thẳng.
Đúng 0
Bình luận (0)
Cho tập hợp A{3;e;7} và B{1;3;7;e}a) Điền các kí hiệu
∈
,
∉
,
⊂
thích hợp vào chỗ chấm sau:
7......
A
1......
A
e
......
A
A
......
B
3
,
7
......
A
1
,
3
,
e
.........
Đọc tiếp
Cho tập hợp A={3;e;7} và B={1;3;7;e}
a) Điền các kí hiệu ∈ , ∉ , ⊂ thích hợp vào chỗ chấm sau:
7...... A 1...... A e ...... A A ...... B 3 , 7 ...... A 1 , 3 , e ...... B
b) Tập hợp B có bao nhiêu phần tử?
a)
7 ∈ A 1 ∉ A e ∈ A A ⊂ B 3 , 7 ⊂ A 1 , 3 , e ⊂ B
b) Tập hợp B gồm có 4 phần tử.
Đúng 0
Bình luận (0)
a) cho các số 57, 85, 357, 814, 3651
a1: Viết tập hợp A các số chia hết cho 3
a2: Viết tất cả các tập hợp con có hai phân tử của tập hợp A.
b/ Viết tập hợp B các số tự nhiên chia hết cho 5, lớn hơn 12 và không vượt quá 99. Tìm số phần tử của tập hợp B.
Giải hộ giúp e. E cảm ơn
Xem chi tiết
a1: A = {57;357;3651}
a2: B = {57;85} ; C = {57;357} ; D = {57;814} ; E = {57;3651} ; G = {85;357} ; H = {85;814} ; L = {85;3651} ; K = {357;814} ; O = {357;3651}
M = {814;3651}
b/ B = {15;20;25;30;35;40;45;50;55;60;65;70;75;80;85;90;95}
Có: (95 - 15) : 5 + 1 = 17 (phần tử)
Trong không gian tọa độ Oxyz, cho hai điểm
A
1
;
-
2
;
-
2
;
B
2
;
2
;
1
. Tập hợp các điểm M thỏa mãn
O
M
→...
Đọc tiếp
Trong không gian tọa độ Oxyz, cho hai điểm A 1 ; - 2 ; - 2 ; B 2 ; 2 ; 1 . Tập hợp các điểm M thỏa mãn O M → ; O A → = O M → ; O B → là một mặt phẳng có phương trình
A. x + 4 y + 3 z = 0
B. 4 x - y + 3 z = 0
C. 3 x + 4 y + 3 z = 0
D. x - 4 y - 3 z = 0
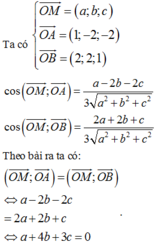
Vậy tập hợp các điểm M thỏa mãn yêu cầu bài toán thuộc mặt phẳng x + 4 y + 3 z = 0
Chọn A.
Đúng 0
Bình luận (0)