Qua tiêu điểm M của đoạn thẳng AB, kẻ đường thẳng Đ vuông góc với AB. lấy điểm K thuộc Đ chứng minh KM là tia phân giác góc AKB
Mọi người làm ơn giúp mình với còn 1 tuần nũa là mình phải nộp rồi !giúp mình lấy điểm 10 với
Những câu hỏi liên quan
Đề bài: Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM à tia phân giác của góc AKB. vẽ hình giúp mình với!
Ta có hình vẽ :
Xét 2 tam giác KAM và KBM ta có :
AM = BM
KM chung
AMK = BMK = 90 độ
\(\Rightarrow\)Tam giác AMK = Tam giác BMK
\(\Rightarrow\)AKM = BKM
\(\Rightarrow\)KM là phân giác của góc AKB .
Đúng 0
Bình luận (0)
ai đổi acc bb4399 kb học gì tầm này
Xem thêm câu trả lời
Qua trung điểm M của đoạn AB, kẻ đường thẳng vuông góc với AB lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB
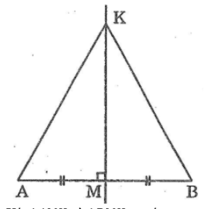
Xét ΔAMK và ΔBMK, ta có:
AM = BM (gt)
∠(AMK) =∠(BMK) =90o (vì KM⊥AB)
MK cạnh chung
Suy ra: ΔAMK= ΔBMK(c.g.c)
⇒∠(AKM) =∠(BKM)
Vậy KM là tia phân giác của góc AKB
Đúng 0
Bình luận (0)
Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB ?
Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB
Qua trung điểm M của đoạn thẳng AB kẻ đường thẳng vuông góc với AB trên đường thẳng đó lấy K. Chứng minh KM là tia phân giác của góc AKB
Bài1: Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB .
Ta có hình vẽ sau:
Ta có: \(\widehat{M_1}\) + \(\widehat{M_2}\) = 180o hay \(\widehat{M_1}\) + 90o = 180o
\(\Rightarrow\) \(\widehat{M_1}\) = 180o - 90o = 90o
\(\Rightarrow\) \(\widehat{M_1}\) = \(\widehat{M_2}\) = 90o
Xét ΔKAM và ΔKBM có:
KM: Cạnh chung
\(\widehat{M_1}\) = \(\widehat{M_2}\) = 90o (cm trên)
AM = BM (gt)
\(\Rightarrow\) ΔKAM = ΔKBM (c.g.c)
\(\Rightarrow\) \(\widehat{K_1}\) = \(\widehat{K_2}\) (2 góc tương ứng)
\(\Rightarrow\) KM là tia phân giác của \(\widehat{AKB}\) (đpcm)
Đúng 0
Bình luận (0)
Gọi đường thẳng đó là x
Ta có hình vẽ:
Vì \(\widehat{AMK}\) +\(\widehat{BMK}\) = 1800 (kề bù)
Mà KM \(\perp\)AB => \(\widehat{AMK}\)=\(\widehat{BMK}\)=\(\frac{180^0}{2}\)=900
Vậy KM là phân giác góc AKB (đpcm)
Đúng 0
Bình luận (0)
Xét t/g AMK và t/g BMK có:
góc KMA=KMB=90độ (gt)
AM=MB(gt)
KM là cạnh chung
Vậy t/g AMK=t/g AMB(c-g-c)
=>góc AKM=góc BKM(2 góc tương ứng)
mà KM nằm giữa AK và KB
=>KM là tia phân giác của góc AKB
Đúng 0
Bình luận (0)
Qua chung điểm M của đoạn thẳng AB kẻ đường thẳng vuông góc với AB trên đường thẳng đó lấy điểm K. Chứng minh rằng KM là tia phân giác của góc AKB.
qua trung điểm M của đoạn thẳng AB kẻ đường thẳng d vuông góc với AB. trên đường thẳng d lấy hai điểm H và K sao cho M là trung điểm của HK. chứng minh ab là phân giác của góc HAK và HK là tia phân giác cua góc AHB !!!!!!!!!!!!!!!!!!!!!!
GIÚP MK VỚI VẼ CẢ HÌNH VÀ GT KL NŨA NHÉ CẢM ƠN NHIỀU ^_^ !!!!
Qua trung điểm M của đoạn thẳng AB, kẻ đường thẳng vuông góc với AB. Trên đường thẳng đó lấy điểm K.Chứng minh rằng KM là tia phân giác của góc AKB.
Có cần minh giả dùm ko