Cho tam giác ABC vuông tại A đặt AB= c; AC=b. Gọi M là điểm tùy ý trên cạnh BC sao cho góc MAB = α (0< α<90)
CM: AM=\(\frac{bc}{b.cos\text{ }\text{α}+c.sin\text{α}}\)
cho tam giác ABC vuông tại A (AB<AC) đường cao AH. Đặt BC=a, CA=b, AB=c, AH=h. cm tam giác có các cạnh a-h, b-c,h là 1 tam giác vuông
dùng Pitago đảo thử từng cặp 1 thôi:v
ta có: \(\left(b-c\right)^2+h^2=b^2+c^2-2bc+h^2\)(1)
vì tam giác ABC vuông ở A có đường cao AH nên \(a^2=b^2+c^2\)và\(AB.AB=AH.BC=2S\)hay\(b.c=a.h\)
\(\Rightarrow b^2+c^2-2bc+h^2=a^2-2ah+h^2=\left(a-h\right)^2\)
Cho tam giác ABC vuông tại A với AB<AC. Đặt BC=a, CA=b, AB=c. Giả sử a2=4bc. Tính số đo các góc nhọn của tam giác ABC
Cho tam giác ABC vuông tại A. Điểm I là trung điểm của cạnh BC. Qua I kẻ đường thẳng song song với AB cắt AC tại N và kẻ đường thẳng song song với AC cắt AB tại M. Tam giác ABC có thêm điều kiện gì thì tứ giác AMIN là hình vuông?
Cho tam giác ABC. O là giao điểm các đường phân giác. Ta đặt AB=c, AC=b, BC=a. AO cắt BC tại D. Tính DB theo a, b, c
1Cho tam giác ABC vuông tại A biết AH vuông góc với BC, AH = 2HC , HC= 12cm. Tính AB?
2 CHO TAM GIÁC ABC VUÔNG TẠI A BIẾT AH VUÔNG GÓC VỚI BC BIẾT DIỆN TÍCH TAM GIÁC AHC= 54CM^2 VÀ DIỆN TÍCH TAM GIÁC ABC= 96CM^2. TÍNH BC?
3, CHO TAM GIÁC ABC VUÔNG TẠI A BIẾT AH VUÔNG GÓC VỚI BC ,GỌI I, K LẦN LƯỢT LÀ HÌNH CHIẾU CỦA H TRÊN AB, AC. ĐẶT AB= c, AC = b.
a, tính AI , AK theo b, c
b, CMR : BI : CK = c^3 : b^3
Mọi người giúp em với ạ. Em cảm ơn nhiều ạ
cho tam giác ABC, đặt BC =a, CA = b, AB = c. các dường phân giác BD,CE cắt nhau tại I. biết BD.CE= 2BI.CI. tính cá tỉ số BI/BD, CI/CE theo a,b,c rồi suy ra tam giác ABC vuông tại A
qwdddddddddddddddđqqqddddddddddddddddddddddddddddddddddddd09U*(9w bi uehvuhytgvguvh eogeohseydđ qddddddasdewd 7fh 89
em chịu nha chứ ko phải em nhưa mấy bạn kia đâu vì em mới
học lớp 5 hà
cho tam giác ABC vuông tại A, có BC=15 cm , AB=9 cm. Tính độ dài AC và so sánh các góc của tam giác ABC, kẻ HM vuông góc với AC. TRên tia đối của tia MH đặt K sao cho MK=MH.Chứng minh tam giác MHC= tam giác MKB và BK//AC c) vẽ BH cắt AM tại G.Chứng minh GA+GB+GC>18cm
a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=BC^2-AB^2=15^2-9^2=144\)
hay AC=12(cm)
Vậy: AC=12cm
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền AB = R. Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C.
A. 3 5 G m 2 R 2
B. 6 5 G m 2 R 2
C. 12 G m 2 R 2
D. 6 G m 2 R 2
Cho tam giác vuông cân ABC vuông tại C,có cạnh huyền A B = R . Tại ba đỉnh A, B và C của tam giác, người ta đặt 3 chất điểm có khối lượng lần lượt là m, 2m và 3m. Tìm lực hấp dẫn tác dụng lên chất điểm tại C.
A. 3 5 G m 2 R 2
B. 6 5 G m 2 R 2
C. 12 G m 2 R 2
D. 5 5 G m 2 R 2
Chọn B.
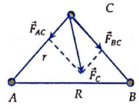
Vì tam giác ABC cân tại C nên ta có AC=BC= R 2
Lực hấp dẫn tác dụng lên chất điểm tại
![]()
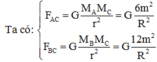
![]()
1. Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC tại H. CM: DE>BC.
2. Cho tam giác ABC cân tại A . Trên cạnh AB đặt đoạn BD và trên tia đối của tia CA đặt đoạn CE sao cho BD=CE. CM: DE>BC.
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)