tìm các căn bậc 2 của 16
Những câu hỏi liên quan
Tìm căn bậc hai không âm của các số sau: 16; 1600;0,16; 162
Câu 1: Tính giá trị các biểu thức:a) . b) . c) . d) .Câu 2: Tìm căn bậc hai của các số sau:a) 16. b) . c) . d) .Câu 3: Tìm căn bậc hai số học của các số sau:a) 625. b) . c) . d).Câu 4: Tìm giá trị của biết:a...
Đọc tiếp
Câu 1: Tính giá trị các biểu thức:
a) 
. b) 
. c) 
. d) 
.
Câu 2: Tìm căn bậc hai của các số sau:
a) 16. b) 
. c) 
. d) 
.
Câu 3: Tìm căn bậc hai số học của các số sau:
a) 625. b) 
. c) 
. d)
.
Câu 4: Tìm giá trị của 
biết:
a) 
. b) 
. c) 
. d) 
.
Câu 5: Tìm số thỏa mãn:
a) 
. b) 
. c) 
. d) 
.
Câu 6: Tìm , biết:
a) 
. b) 
. 
Dạng 2: So sánh các căn bậc hai số học
Câu 1: Không dùng máy tính, so sánh các số sau:
a) 
và 3. b) 
và 
. c) 
và 2.
Câu 2: Không dùng máy tính, hãy so sánh các số thực sau:
a) 
và 6. b) 
và 
.
Câu 3: So sánh các số sau:
a) 
và 2. b) 
và 
.
Câu 4: Không dùng máy tính, hãy so sánh các số thực sau:
a) 
và 9. b) 
và 
.
c) 
và 
. d) 
và 
.
e) 
và 
. f) 
và 
.
căn bậc hai của (3X2-12X-16) + căn bậc hai của (Y2-4Y+13) = 5
Tìm X,Y
Tìm căn bậc hai của 16
Ta có : 42 = 16 và (-4)2 = 16
Nên 4 và – 4 là các căn bậc hai của 16
Đúng 0
Bình luận (0)
Trong các số sau đây số nào có căn bậc hai? Hãy cho biết căn bậc hai không âm của các số đó:
a = 0 b = -25 c = 1
d = 16 + 9 e = 32 + 42 g = π -4
h = (2-11)2 i = (-5)2 k = -32
l = √16 m = 34 n = 52 - 32
Các số có căn bậc hai:
a = 0 c = 1 d = 16 + 9
e = 32 + 42 h = (2-11)2 i = (-5)2
l = √16 m = 34 n = 52 - 32
Căn bậc hai không âm của các số đó là:
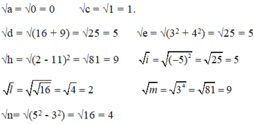
Đúng 0
Bình luận (0)
tìm gtnn củ căn bậc 2 x2+16 -8
cho A=căn bậc 2 của x+1/căn bậc 2 của x-1
tính A biết x=16/9
- Ta có: \(A=\frac{\sqrt{x+1}}{\sqrt{x-1}}\)
- Thay \(x=\frac{16}{9}\)vào đa thức \(A,\)ta có:
\(A=\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}\)
\(\Leftrightarrow A=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}\)
\(\Leftrightarrow A=\frac{5\sqrt{7}}{7}\)
Vậy \(A=\frac{5\sqrt{7}}{7}\)
Thay x = 16/9 vào biểu thức, ta có:
\(\frac{\sqrt{\frac{16}{9}+1}}{\sqrt{\frac{16}{9}-1}}=\frac{\sqrt{\frac{25}{9}}}{\sqrt{\frac{7}{9}}}=\frac{\frac{5}{3}}{\frac{\sqrt{7}}{3}}=\frac{5\sqrt{7}}{5}\)
Câu 4: Tính và so sánh
a. căn bậc 81 phần căn bậc 16 và 81 16
b.căn bậc 16+ 25 và căn bậc 16 + căn bậc 25
a: \(\dfrac{\sqrt{81}}{\sqrt{16}}=\dfrac{9}{4}=\dfrac{36}{16}< \dfrac{81}{16}\)
b: \(\sqrt{16+25}=\sqrt{41}< 9=\sqrt{16}+\sqrt{25}\)
Đúng 0
Bình luận (0)
Từ các số là bình phương của 12 số tự nhiên đầu tiên, em hãy tìm căn bậc hai số học của các số sau:
a) 9; b) 16;
c) 81; d) 121
a) Vì \({3^2} = 9\) và 3 > 0 nên \(\sqrt 9 = 3\)
b) Vì \({4^2} = 16\) và 4 > 0 nên \(\sqrt {16} = 4\)
c) Vì \({9^2} = 81\) và 9 > 0 nên \(\sqrt {81} = 9\)
d) Vì \({11^2} = 121\) và 11 > 0 nên \(\sqrt {121} = 11\)
Đúng 1
Bình luận (0)