Từ mỗi đỉnh dựng được 3 vectơ khác 0 →  nhận đỉnh đó làm điểm đầu, điểm cuối là các đỉnh còn lại. Suy ra từ 4 đỉnh có 12 vectơ.

Đáp án C

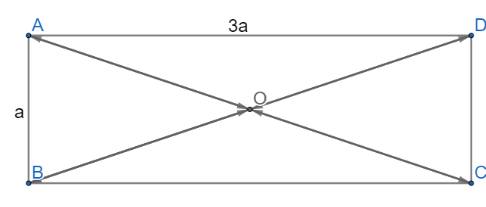
a) Ta có:

\(AC = BD = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{a^2} + {{\left( {3a} \right)}^2}}  = a\sqrt {10} \)

+) \(\left| {\overrightarrow {AC} } \right| = AC = a\sqrt {10} \)

+) \(\left| {\overrightarrow {BD} } \right| = BD = a\sqrt {10} \)

b) O là giao điểm của hai đường chéo nên ta có:

\(AO = OC = BO = OD = \frac{{a\sqrt {10} }}{2}\)

Dựa vào hình vẽ ta thấy AO và CO cùng nằm trên một đường thẳng; BO và DO cùng nằm trên một đường thẳng

Suy ra các cặp vectơ đối nhau và có độ dài bằng \(\frac{{a\sqrt {10} }}{2}\) là:

\(\overrightarrow {OA} \) và \(\overrightarrow {OC} \); \(\overrightarrow {AO} \) và \(\overrightarrow {CO} \); \(\overrightarrow {OB} \) và \(\overrightarrow {OD} \); \(\overrightarrow {BO} \) và \(\overrightarrow {DO} \)

Trong hình chữ nhật, các cạnh đối diện bằng nhau và hai đường chéo bằng nhau nên ta có ba nhóm vectơ có độ dài bằng nhau, đó là:

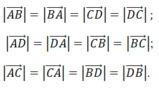
Đáp án B

\(\overrightarrow{AO}=\overrightarrow{OC};\overrightarrow{DO}=\overrightarrow{OB}\);
\(\overrightarrow{OA}=\overrightarrow{CO};\overrightarrow{DO}=\overrightarrow{OB}\).

Các nhóm vecto bằng nhau là: 

Đáp án B

12

Số các véc tơ tạo thành từ 4 điểm A, B, C, D đúng bằng số đoạn thẳng tạo thàng từ 4 điểm đó nhân với 2.
Số đoạn thẳng là: \(4.3:2=6\) (đoạn).
Số véc tơ là: 6.2 = 12 (véc tơ).
Tổng quát:
Số véc tơ tạo thành từ n điểm là: \(n\left(n-1\right)\) (véc tơ).

I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)

\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:

\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)

Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt

Phương trình AB:

\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)

B là giao điểm AB và BC nên tọa độ là nghiệm:

\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)

I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)

8

Số các véc tơ khác \(\overrightarrow{0}\) bằng véc tơ \(\overrightarrow{OC}\) có điểm đầu và điểm cuối là đỉnh lục giác là:
\(\overrightarrow{AB};\overrightarrow{BA};\overrightarrow{FO};\overrightarrow{OF};\overrightarrow{ED};\overrightarrow{DE};\overrightarrow{FC};\overrightarrow{CF}\).
Có 8 véc tơ.

AB đi qua E và vuông góc BC nên nhận (1;-1) là 1 vtpt

Phương trình AB:

\(1\left(x+1\right)-1\left(y-1\right)=0\Leftrightarrow x-y+2=0\)

Tọa độ B là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(-3;-1\right)\)

Đường thẳng d qua M và song song AB có pt:

\(1\left(x+1\right)-1\left(y+1\right)=0\Leftrightarrow x-y=0\)

Gọi N là giao điểm d và BC \(\Rightarrow N\) là trung điểm BC

Tọa độ N là nghiệm: \(\left\{{}\begin{matrix}x-y=0\\x+y-4=0\end{matrix}\right.\) \(\Rightarrow N\left(2;2\right)\Rightarrow C\left(7;5\right)\)

Đường thẳng AD qua M và song song BC có pt:

\(1\left(x+1\right)+1\left(y+1\right)=0\Leftrightarrow x+y+2=0\)

A là giao điểm AB và AD nên tọa độ là nghiệm: \(\left\{{}\begin{matrix}x-y+2=0\\x+y+2=0\end{matrix}\right.\) \(\Rightarrow A\left(-2;0\right)\)

\(\overrightarrow{AB}=\overrightarrow{DC}\Rightarrow\) tọa độ D