Đường thẳng d tiếp xúc đường tròn nghĩa là tiếp tuyến đk bạn? Vì mình nghĩ nếu ko phải tiếp tuyến thì ko đủ để tìm đâu

Áp dụng Pytago cho tam giác ABC vuông tại B

\(AC=\sqrt{AB^2+BC^2}=\sqrt{3^2+4^2}=5\left(cm\right)\)

Vì \(\widehat{AMB}=90^0\) (góc nt chắn nửa đường tròn) nên \(BM\perp AC\)

Áp dụng HTL tam giác \(AB^2=AM\cdot AC\Rightarrow AM=\dfrac{AB^2}{AC}=\dfrac{16}{5}=3,2\left(cm\right)\)

Vì d tiếp xúc với đường tròn (O) tại B 

=> AB vuông BC 

=> ^ABC = 90⁰ ( t/c tiếp tuyến ) 

Lại có : M thuộc (O) ; AB là đường kính

=> ^AMB = 90⁰ ( t/c điểm thuộc đường tròn nhìn đường kính ) 

=> BM vuông AC 

Áp dụng định lí Pytago tam giác ABC vuông tại B 

\(AC=\sqrt{AB^2+BC^2}=\sqrt{16+9}=5\)cm 

Xét tam giác ABC vuông tại B, đường cao BM 

* Áp dụng hệ thức : \(AB^2=AM.AC\Rightarrow AM=\frac{AB^2}{AC}=\frac{16}{5}\)cm 

 cho xin 1 t

1: góc ACB=góc ADB=1/2*sđ cung AB=90 độ

=>AC vuông góc CB và AD vuông góc DB

=>góc ECM=90 độ=góc EDM

=>CEDM nội tiếp

AC vuông góc CB

AD vuông góc DB

=>AD,BC là 2 đường cao của ΔAEB

=>M là trực tâm

=>AM vuông góc AB

ΔMDB vuông tại D nên ΔMDB nội tiếp đường tròn đường kính MB

=>BM là đường kính của (I)

=>góc MNB=90 độ

=>MN vuông góc AB

=>E,M,N thẳng hàng

b: AM vuông góc AB

=>góc ANM=90 độ

góc ANM+góc ACM=180 độ

=>ACMN nội tiếp

=>góc CAM=góc CNM=góc ADF

=>góc CAM=góc ADF

=>DF//AB

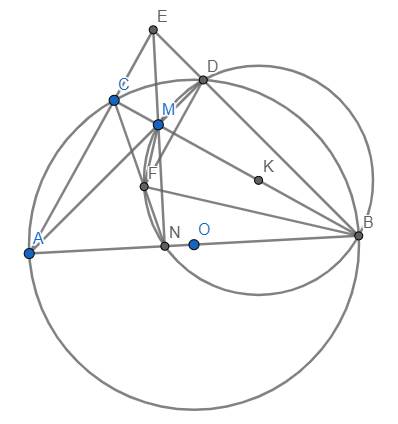
a) Tứ giác BDFN nội tiếp nên \(\widehat{CNA}=\widehat{BDF}\) (*)

 Xét đường tròn (K), đường kính BM, ta có \(\widehat{MNB}=90^o\)  hay \(MN\perp AB\) tại N (1)

 Với lí do tương tự, ta có \(AD\perp EB,BC\perp EA\), do đó M là trực tâm của tam giác EAB \(\Rightarrow EM\perp AB\)  (2)

 Từ (1) và (2) \(\Rightarrow\) M, N, P thẳng hàng và đường thẳng này vuông góc với AB.

 Từ đó suy ra tứ giác BECN nội tiếp (vì \(\widehat{ECB}=\widehat{ENB}=90^o\))

 \(\Rightarrow\widehat{CNA}=\widehat{AEB}\) (**)

Từ (*) và (**), suy ra \(\widehat{BDF}=\widehat{BEA}\) \(\Rightarrow\) DF//AE (đpcm)

b) Tương tự như trên, ta có tứ giác AEDN nội tiếp \(\Rightarrow\widehat{BND}=\widehat{AEB}\), dẫn đến \(\Delta BDN~\Delta BAE\left(g.g\right)\) \(\Rightarrow\dfrac{BD}{BA}=\dfrac{BN}{BE}\Rightarrow BD.BE=BA.BN\) (3)

 Tứ giác NBMD nội tiếp nên \(\widehat{ANM}=\widehat{ADB}\), dẫn đến \(\Delta AMN~\Delta ABD\left(g.g\right)\) 

 \(\Rightarrow\dfrac{AM}{AB}=\dfrac{AN}{AD}\Rightarrow AD.AM=AB.AN\)  (4)

Cộng theo vế (3) và (4), thu được \(BD.BE+AM.AD=AB.BN+AB.AN=AB\left(BN+AN\right)=AB^2=4R^2\)không thay đổi. (đpcm)