Cho tam giác ABC có điểm N thuộc cạnh AC ,M thuộc cạnh BC .Gọi I là giao điểm của AM và BN .hãy kể tên các bộ ba điểm , xác định điểm nằm giữa hai điểm còn lại trong mỗi trường hợp .

Những câu hỏi liên quan
Cho tam giác ABC điểm M thuộc cạnh BC điểm I thuộc cạnh AM gọi K là giao điểm của CI và AB tính AB/BK trong các trường hợp sau:
a) BM=CM; AI=MI
b) AI/MI=3/4
Giúp mik vs mọi người ơi:)))
Cho tam giác ABC có
B
A
C
^
90°. Lấy điểm M thuộc cạnh BC sao cho
M
A
C
^
20°.a) Tính
M
A
B
^
.b) Trong góc
M
A
B
^
vẽ tia...
Đọc tiếp
Cho tam giác ABC có B A C ^ = 90°. Lấy điểm M thuộc cạnh BC sao cho M A C ^ = 20°.
a) Tính M A B ^ .
b) Trong góc M A B ^ vẽ tia Ax cắt BC tại N sao cho N A B ^ = 50°. Trong ba điểm N, M, C điểm nào nằm giữa hai điểm còn lại?
c) Chứng tỏ AM là tia phân giác của góc N A C ^
a) M A B ^ = 70°.
b) Trong ba điểm N, M, C điểm M nằm giữa hai điểm còn lại
c) AM là tia phân giác của góc N A C ^ vì tia AM nằm giũa hai tia AN,AC và N A M ^ = M A C ^
Đúng 0
Bình luận (0)
a) Vì tia AM nằm giữa hai tia AB và AC, nên ta có:
ˆMAB+ˆMAC=ˆBACMAB^+MAC^=BAC^
⇒ˆMAB=ˆBAC−ˆMAC=90o−20o⇒MAB^=BAC^−MAC^=90o−20o
⇒ˆMAB=70o⇒MAB^=70o
b) Trong 3 điểm N, M, C điểm M nằm giữa hai điểm còn lại vì CM < CN.
c) Vì tia AN nằm giữa hai tia AB và AC, nên ta có:
ˆNAB+ˆNAC=ˆBACNAB^+NAC^=BAC^
⇒ˆNAC=ˆBAC−ˆNAB=90o−50o⇒NAC^=BAC^−NAB^=90o−50o
⇒ˆNAC=40o⇒NAC^=40o
Ta có AM nằm giữa hai tia AN và AC (1)
Và
Đúng 0
Bình luận (0)
Cho tam giác ABC có
B
A
C
^
90
°
.
Lấy điểm M thuộc cạnh BC sao cho
M
A
C
^
20
°
.a) Tính
M
A
B...
Đọc tiếp
Cho tam giác ABC có B A C ^ = 90 ° . Lấy điểm M thuộc cạnh BC sao cho M A C ^ = 20 ° .
a) Tính M A B ^ .
b) Trong góc M A B ^ vẽ tia Ax cắt BC tại N sao cho N A B ^ = 50 ° . Trong ba điểm N, M, C điểm nào nằm giữa hai điểm còn lại?
c) Chứng tỏ AM là tia phân giác của góc N A C ^
a) M A B ^ = 70 °
b) Trong ba điểm N, M, C điểm M nằm giữa hai điểm còn lại
c) AM là tia phân giác của góc N A C ^ vì tia AM nằm giũa hai tia AN,AC và N A M ^ = M A C ^
Đúng 0
Bình luận (0)
Cho tam giác ABC. Xét các điểm M thuộc BC, N thuộc CA và P thuộc AB sao cho tứ giác APMN là một hình bình hành. Gọi O là giao điểm của các đường thẳng BN và CP. Xác định vị trí hình học của điểm M trên cạnh BC sao cho góc PMO= góc OMP
Gọi D là đỉnh thức tư của hình bình hành ABDC. Khi đó, O, M, D thẳng hàng.
Do giả thiết nên DB//MP, DC//MN. Từ đó, do O, M, D thẳng hàng, nên góc PMO = góc OMN <=> OM là phân giác góc PMN <=> DM là phân giác góc BDC
\(\Leftrightarrow\frac{MB}{MC}=\frac{DB}{DC}\)
Nhưng tứ giác ABDC là một hình bình hành nên BD = AC, CD = AB
do đó : \(\frac{DB}{DC}=\frac{AC}{AB}\)
Vì vậy :
góc PMO bằng góc OMN \(\Leftrightarrow\frac{MB}{MC}=\frac{AC}{AB}\)
Vậy với M là điểm trên cạnh BC sao cho \(\frac{MB}{MC}=\frac{AC}{AB}\) (hay M đối xứng với chân phân giác trong góc BAC qua trung điểm cạnh BC) thì góc PMO bằng góc OMN => Điều cần chứng minh
Đúng 1
Bình luận (2)
Cho tam giác ABC có diện tích 120 cm2. M là điểm thuộc cạnh BC sao cho BM= MC, điểm N thuộc cạnh AC sao cho AN=1/3 AC. Gọi giao điểm của AM và BN là Q .
a) Tính diện tích tam giác ABN, tam giác BMN.
b) Chứng minh AQ=QM.
Cho tam giác ABC vuông tại A có đường phân giác BM(M thuộc AC).Trên cạnh BC lấy điểm N sao cho BN=BA.Gọi K là giao điểm của các đường thẳng AB và MN
a)Chứng minh:MA=MN và BM+AN<AB+3MN
b)Gọi I là trung điểm của đoạn thẳng KC.Chứng minh ba điểm B,M,I thẳng hàng
Giúp mình bài này với mình cảm ơn ạ
a: Xét ΔBAMvà ΔBNM có
BA=BN
góc ABM=góc NBM
BM chung
=>ΔBAM=ΔBNM
=>MA=MN
b: Xét ΔBNK vuông tại N và ΔBAC vuông tại A có
BN=BA
góc NBK chung
=>ΔBNK=ΔBAC
=>BK=BC
Xét ΔMAK vuông tại A và ΔMNC vuông tại N có
MA=MN
góc AMK=góc NMC
=>ΔMAK=ΔMNC
=>MK=MC
=>BM là trung trực của CK
=>B,M,I thẳng hàng
Đúng 0
Bình luận (0)
Cho tứ diện ABCD và điểm M thuộc miền trong của tam giác ACD . Gọi I và J tương ứng là hai điểm trên cạnh BC và BD sao cho IJ không song song với CD
a) Hãy xác định giao tuyến của hai mặt phẳng (IJM) và (ACD).
b) Lấy N là điểm thuộc miền trong của tam giác ABD sao cho JN cắt đoạn AB tại L. Tìm giao tuyến của hai mặt phẳng (MNJ) và (ABC)
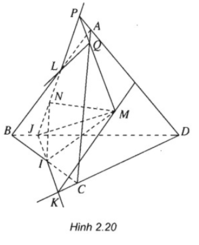
a) Nhận xét:
Do giả thiết cho IJ không song song với CD và chúng cùng nằm trong mặt phẳng (BCD) nên khi kéo dài chúng gặp nhau tại một điểm.
Gọi K = IJ ∩ CD.
Ta có: M là điểm chung thứ nhất của (ACD) và (IJM);
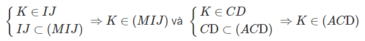
Vậy (MIJ) ∩ (ACD) = MK
b) Với L = JN ∩ AB ta có:
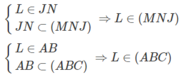
Như vậy L là điểm chung thứ nhất của hai mặt phẳng (MNJ) và (ABC)
Gọi P = JL ∩ AD, Q = PM ∩ AC
Ta có:
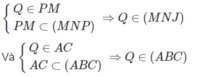
Nên Q là điểm chung thứ hai của (MNJ) và (ABC)
Vậy LQ = (ABC) ∩ (MNJ).
Đúng 0
Bình luận (0)
Cho tam giác ABC, gọi M là điểm thuộc cạnh AB, N là điểm thuộc cạnh AC sao cho 3AM = AB; 4AN = 3AC . Gọi O là giao điểm của CM và BN. Trên đường thẳng BC lấy điểm E và đặt \(\overrightarrow{BE}=x\overrightarrow{BC}\) .Xác định x để A; O; E thẳng hàng
Cho 2 tia đối nhau AB và AC
a)Gọi M là điểm thuộc tia AB.trong ba điểm A,B,M thì điểm nào nằm giữa hai điểm còn lại ? vì sao?
b)Lấy N thuộc tia AC, kể tên các tia đối nhau gốc N, các tia trùng gốc N
c)Trong ba điểm A,B,C thì điểm nào nằm giửa hai điểm còn lại














