Cho hình vuông ABCD. Tính cos MAN biết rằng M, N theo thứ tự là trug điểm của BC, CD.

Những câu hỏi liên quan
Cho hình vuông ABCD. Tính cos góc MAN biết rằng M, N theo thứ tự là trung điểm của BC, C
cho hình vuông ABCD . biết M và N theo thứ tự là trung điểm của BC và CD biết tam giác AMD cân tại M . tính COS góc MAN
Cho hình thang cân ABCD ( AB // CD ) .Gọi M , N , P , Q theo thứ tự là trug điểm AB , BC , CD , DA
a) C/m tg MNPQ là h.thoi
b) Hình thang cân ABCD cần thêm điều kienj gì để tg MNPQ là hình vuông?
a,
Xét ABD, ta có :
MA = MB (gt)
QA = QD (gt)
=> MQ là đường trung bình.
=> MQ // BD và MQ = BD : 2 (1)
Cmtt, ta được :
NP // BD và NP = BD : 2 (2)
NM // AC và NM = AC : 2 (3)
Từ (1) và (2) : MQ // NP và MQ = PP
=> Tứ giác MNPQ làhình bình hành.
ta có :
AC = BD ( hai đường chéo hình thang cân ABCD)
NM = AC : 2 (cmt)
MQ = BD : 2 (cmt)
=> NM = MQ
Xét hình bình hành MNPQ, ta có :
NM = MQ (cmt)
=> hình bình hành MNPQ là hình thoi.
b , Nếu AC BD
NM // AC (cmt)
NP // BD (cmt)
=> NM NP tại N
Hay
Xét hình thoi MNPQ , ta có : (cmt)
=> hình thoi MNPQ là hình vuông.
tick nha bn
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính cos(MAN).
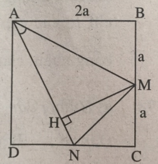
Kẻ đường cao MH của tam giác cân AMN. Ta có sin ∠ (NAM) = HM/AM và diện tích tam giác AMN là S A M N = 1/2AN.MH = 1/2AN.AM.sin(NAM) = 1/2 A N 2 .sin(NAM) = 1/2( A D 2 + D N 2 ). sin(NAM) = ( 5 a 2 )/2 sin(NAM).
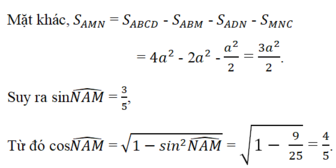
Đúng 1
Bình luận (0)
Cho hình vuông ABCD . gọi M ,N lần lượt là trung điểm của BC và CD. Tính cos góc MAN
Vì \(\tan MAB=\frac{MB}{AB}=\frac{1}{2}\Rightarrow\widehat{MAB}=26,5°\)Tương tự có \(\widehat{NAD}=26,5°\)
\(\Rightarrow\widehat{MAN}=37°\Rightarrow\cos MAN=\cos37\approx0,79\)
Cho hình vuông ABCD có cạnh bằng 2a. Gọi M, N lần lượt là trung điểm của BC, CD. Tính \(\cos\widehat{MAN}\) ?
Chi hình vuông ABCD biết M và N là trung tuyến của BC và CD. Biết tam giác ADM cân tại M . Tính Cos của góc MAN
Cho hình vuông ABCD. Gọi M và N là trung điểm của BC và DC. Tính cos góc MAN
cos(300) =\(\frac{\sqrt{3}}{2}\)
lik-e nha
Đúng 1
Bình luận (0)
Bài 1: Cho tứ giác ABCD và các điểm M,N,P,Q theo thứ tự là trung điểm của AB, BC, CD,DAa. Chứng minh rằng: TỨ giác MNPQ là hình bình hànhb. 2 đường chéo AC và BD phải có điều kiện gì thì MNPQ là hình thoi, hình vuông, hình chữ nhật.Bài 2: Cho tứ giác ABCD biết AC vuông góc với BD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DAa. Tứ giác EFGH là hình gì? Vì sao?b. Tính diện tích tứ giác EFGH biết AC6cm ; BD 4 cmHelp me!
Đọc tiếp
Bài 1: Cho tứ giác ABCD và các điểm M,N,P,Q theo thứ tự là trung điểm của AB, BC, CD,DA
a. Chứng minh rằng: TỨ giác MNPQ là hình bình hành
b. 2 đường chéo AC và BD phải có điều kiện gì thì MNPQ là hình thoi, hình vuông, hình chữ nhật.
Bài 2: Cho tứ giác ABCD biết AC vuông góc với BD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA
a. Tứ giác EFGH là hình gì? Vì sao?
b. Tính diện tích tứ giác EFGH biết AC=6cm ; BD = 4 cm
Help me!
















