vẽ trên cùng một hệ trục tọa độ đồ thị các hàm số sau
y=x(d1);y=2x(d2);d=3-x(d3)
đường thẳng d3 cắt các đường thẳng d1,d2 theo thứ tự A và B.tìm tọa độ điểm A,B.tính diện tích tam giác AOB
Vẽ trên cùng hệ trục tọa độ Oxy đồ thị các hàm số sau đây:
y = x ( d 1 )
y = 2x ( d 2 )
y = -x + 3 ( d 3 )
*Vẽ đồ thị của hàm số y = x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 1
Đồ thị hàm số y = x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1; 1)
*Vẽ đồ thị hàm số y = 2x
Cho x = 0 thì y = 0
Cho x = 1 thì y = 2
Đồ thị hàm số y = 2x là đường thẳng đi qua gốc tọa độ O(0; 0) và điểm (1;2)
*Vẽ đồ thị của hàm số y = -x + 3
Cho x = 0 thì y = 3. Ta có điểm (0; 3)
Cho y = 0 thì x = 3. Ta có điểm (3; 0)
Đồ thị hàm số y = -x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0)
Trong mặt phẳng tọa độ Oxy Cho hàm số y = 2 x - 3 có đồ thị là đường thẳng d1 và hàm số y = 1/2 x có đồ thị là đường thẳng d2 a vẽ đồ thị d1 và d2 trên cùng hệ trục tọa độ
Cho hàm số y = x + 2 và hàm số y = 3 − x có đồ thị là (d1) và )(d2).
a) Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ.
b) Tìm tọa độ giao điểm của (d1) với trục hoành.
c) Tìm tọa độ giao điểm của (d2) với trục tung.
d) Tìm tọa độ giao điểm của (d1) và (d2).
Cho hàm số y=-x có đồ thị (D1) và hàm số y=2x-3 có đồ thị (D2)
a)Vẽ (D1), (D2) trên cùng một hệ trục tọa độ. Tìm tọa độ giao điểm của (D1), (D2) bằng phép toán
b)Cho (D3):y=(2k-1)x+3-k. Tìm k để (D1), (D2) và (D3) đồng quy
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau: y = - x
Vẽ hệ trục tọa độ Oxy
Với x = 1 ta được y = -1. Điểm A(1 ;-1) thuộc đồ thị của hàm số y = -x
Vậy đường thằng OA là đồ thị hàm số y = -x
Vẽ đồ thị của các hàm số sau trên cùng một hệ trục tọa độ:
y = |x|;
y = |x + 1|.
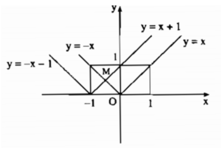
Ta vẽ đồ thị y = x với x ≥ 0.
Vẽ đồ thị y = -x với x ≤ 0.
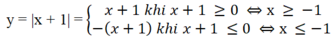
Ta vẽ đồ thị y = x + 1 với x ≥ -1
Vẽ đồ thị y = -x – 1 với x ≤ -1.
Bài 1: Tìm m để a/ Hàm số y = (- m + 4) x + 5 là hàm số bậc nhất b/ Hàm số y = (2 - m) x - 3 đồng biến trong R Bài 2: Cho hàm số y = 2x có đồ thị (d1); hàm số y=x-1 có đồ thị (d2) . a / Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ. b/ Xác định tọa độ giao điểm A của (d1) và (d2) bằng phép toán. c/ Viết ph / trình đường thẳng (D) song song với (d2) và điểm M(6;3) qua
b: Để hàm số đồng biến thì 2-m>0
hay m<2
Cho hàm số y=3x-1 có đồ thị d1 và hàm số y=-x +3 có đồ thị d2 A. Vẽ đồ thị hs trên cùng hệ trục tọa độ Oxy B. Gọi giao điểm d1, d2 với trục Õ lần lượt là A và B, giao điểm của 2 đường thẳng d1 và d2 là C. Tìm tọa độ các điểm A,B,C C. Tính số đo của góc tạo bởi đường thẳng d1 với tia Ox
a: 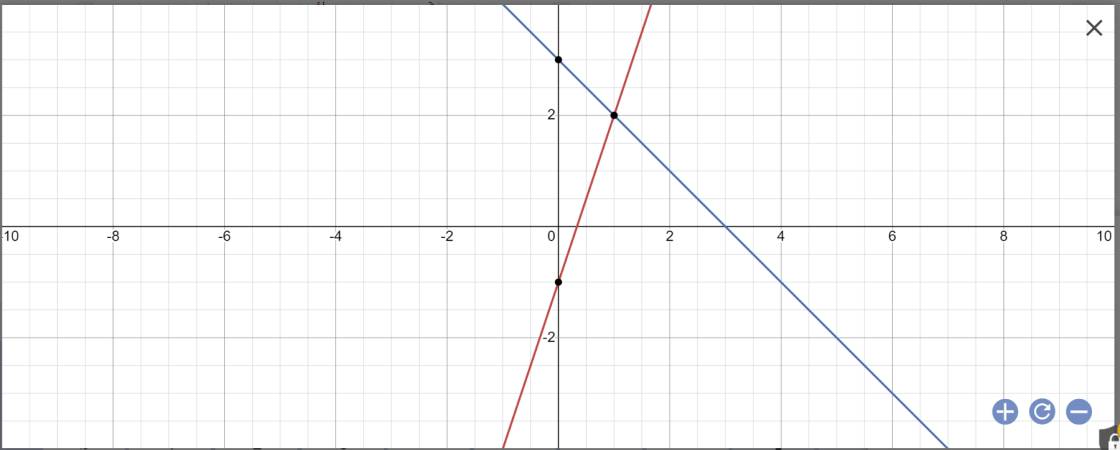
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\3x-1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{1}{3}\\y=0\end{matrix}\right.\)
Vậy: A(1/3;0)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\-x+3=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-x=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=3\end{matrix}\right.\)
Vậy: B(3;0)
Tọa độ C là:
\(\left\{{}\begin{matrix}3x-1=-x+3\\y=3x-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x=4\\y=3x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=3\cdot1-1=2\end{matrix}\right.\)
Vậy: C(1;2)
c: Gọi \(\alpha\) là góc tạo bởi (d1) với trục Ox
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^033'\)
Bài 2: Cho hàm số y = 2x có đồ thị (d1); hàm số y=x-1 có đồ thị (d2) . a / Vẽ (d1) và (d2) trên cùng một hệ trục tọa độ. b/ Xác định tọa độ giao điểm A của (d1) và (d2) bằng phép toán. c/ Viết ph / trình đường thẳng (D) song song với (d2) và điểm M(6;3) qua
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}2x=x-1\\y=x-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=-2\end{matrix}\right.\)
Vẽ trên cùng một hệ trục tọa độ đồ thị của các hàm số sau: y = 1 2 x
Với x = 1 ta được 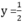 . Điểm B(1 ; 1/2) thuộc đồ thị của hàm số
. Điểm B(1 ; 1/2) thuộc đồ thị của hàm số 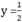 x
x
Vậy đường thằng OB là đồ thị hàm số 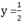 x
x