cho tứ giác abcd gọi m,n,p lần lượt là trung điểm bc,bd,ad,ac chứng minh mnpq là hình bình hành

Những câu hỏi liên quan
Cho hình bình hành ABCD. Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA
a) Chứng minh tứ giác MNPQ là hình bình hành
b) Hình bình hành ABCD cần thêm điều kiện gì để MNPQ là hình chữ nhật, hình thoi, hình vuông?
c) Gọi O là giao điểm của AC,BD.Chứng minh: M,O,P thẳng hàng
d) Chứng minh : AC, BD, QN đồng qui
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của BC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//AC và MN=AC/2(1)
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC và QP=AC/2(2)
Từ (1) và (2) suy ra MN//PQ và MN=PQ
hay MNPQ là hình bình hành
Đúng 1
Bình luận (0)
Cho tứ giác ABCD có ADC+BCD=90° và AD=BC . Gọi M, N, P, Q lần lượt là trung điểm của AB, AC, CD, BD. a) Chúng minh rằng tứ giác MNPQ là hình bình hành. b) đường thẳng PM cắt BC tại E. tính góc PEC. c) chứng minh diện tích MNPQ≥ (AB-CD)²/8. đẳng thức xảy ra khi nào?
PLEASE!❤️🙏
Cho tứ giác ABCD gọi M N P Q lần lượt là trung điểm của các cạnh AB BC CD DA
A) Chứng minh tứ giác MNPQ là hình bình hành
b) tìm điều kiện hai đường chéo AC và BD của tứ giác ABCD để MNPQ là hình chữ nhật
a: Xét ΔBAD có
M,Q lần lượt là tđiểm của AB và AD
nên MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N,P lần lượt là trung điểm của CB và CD
nên NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy a MQ//NP và MQ=NP
=>MNPQ là hình bình hành
b: Xét ΔABC có
M,N lần lượt là trung điểm của BA và BC
nên MN là đường trung bình
=>MN=AC/2 và MN//AC
Để MNPQ là hình chữ nhật thì MN vuông góc với MQ
=>AC vuông góc với BD
Đúng 0
Bình luận (0)
Cho tứ giác ABCD. Gọi M, N, P, Q lần lượt là trung điểm các cạnh AB, BC, CD, DA và I, K là trung điểm các đường chéo AC, BD. Chứng minh :
a) Các tứ giác MNPQ, INKQ là hình bình hành
Giúp mình với nhá, mai mình phải nộp bài rồi!!!
Đúng 0
Bình luận (0)
Cho tứ giác ABCD, gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. a) Chứng minh rằng MNPQ là hình bình hành b) Gọi I, J lần lượt là trung điểm của AC và BD. Chứng minh rằng các đoạn thẳng MP, QN, IJ đồng quy tại một điểm.
a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔABD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
P là trung điểm của CD
N là trung điểm của BC
Do đó: PN là đường trung bình của ΔABD
Suy ra: PN//BD và \(PN=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra MQ//PN và MQ=PN
hay MNPQ là hình bình hành
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Gọi M, N, P, Q, R và S lần lượt trung điểm của AB, CD, BC, AD, AC và BD. Chứng minh rằng tứ giác MNPQ là hình bình hành. Từ đó suy ra ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
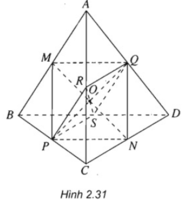
Trong tam giác ABC ta có:
MP // AC và MP = AC/2.
Trong tam giác ACD ta có:
QN // AC và QN = AC/2.
Từ đó suy ra {MP // QN}
⇒ Tứ giác MNPQ là hình bình hành.
Do vậy hai đường chéo MN và PQ cắt nhau tại trung điểm O của mỗi đường.
Tương tự: PR // QS và PR = QS = AB/2. Do đó tứ giác PQRS là hình bình hành.
Suy ra hai đường chéo RS và PQ cắt nhau tại trung điểm O của PQ và OR = OS
Vậy ba đoạn thẳng MN, PQ và RS cắt nhau tại trung điểm mỗi đoạn.
Đúng 0
Bình luận (0)
cho tứ giác ABCD . Gọi E,F lần lượt là giao điểm của AB,CD,AD và BC; M,N,P,Q lần lượt là trung điểm của AE,EC,CF,FA. Chứng minh tứ giác MNPQ là hình bình hành
EP // MF (EP là đường trung bình trong ∆BAF) và EP = AF / 2 = MF => MENF là hình bình hành.
=> MP và EF cắt nhau tại trung điểm I.
FN // DE và FN = DE / 2 = QE => FQEN là hình bình hành => QN và EF cắt nhau tại trung điểm I
=> MP và QN cắt nhau tại trung điểm của chúng => MNPQ là hình bình hành
Đúng 1
Bình luận (1)
Cho tứ giác ABCD . gọi M , N , P , Q , E , G lần lượt là trung điểm của AB , BC , CD , DA , BD , AC .
a) Chứng minh tứ giác MNPQ , MEPG là hình bình hành .
b) Chứng minh MP , NQ , EG là đồng quy
Cho tứ giác ABCD . gọi M , N , P , Q , E , G lần lượt là trung điểm của AB , BC , CD , DA , BD , AC .
a) Chứng minh tứ giác MNPQ , MEPG là hình bình hành .
b) Chứng minh MP , NQ , EG là đồng quy














