Chứng tỏ rằng 2110 -1 chia hết cho 200

Những câu hỏi liên quan
Chứng tỏ rằng 21 10 – 1 chia hết cho 200
* Áp dụng hằng đẳng thức:
![]()
Ta có:
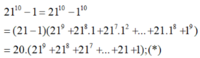
Ta có:
![]()
![]()
gồm có 10 số hạng
![]()
có chữ số tận cùng bằng 0. Do đó, ta có thể viết:
![]()
Thay vào (*) ta được:
2110 - 1 = 20.10.A = 200A
Suy ra: 2110 - 1 chia hết cho 200.
Đúng 0
Bình luận (0)
Chứng minh rằng
a) 2110−1chia hết cho 200
b) 3930+3913chia hết cho 40
c) 260+530chia hết cho 41
link tham khảo
ccaau hỏi của ng duy mạnh
link : https://olm.vn/hoi-dap/detail/60197622644.html
hok tót
Đúng 0
Bình luận (0)
1,Chứng tỏ rằng 2110 – 1 chia hết cho 200
Ta có: 2110 - 1 = (21 - 1)(219 + 218 + 217 + ... + 21 + 1)
= 20.10M (M ∈ N)
= 200.M chia hết cho 200.
Đúng 0
Bình luận (0)
Chứng tỏ rằng biểu thức sau chia hết cho 10:
a)A=(11^200)-1 b)B=(12^300)-(2^300)
a. ta có \(11\equiv1mod10\Rightarrow11^{200}\equiv1mod10\)
nên \(11^{200}-1\equiv0mod10\). Vậy \(11^{200}-1\) chia hết cho 10.
b. ta có \(12\equiv2mod10\Rightarrow12^{200}\equiv2^{200}mod10\)
nên \(12^{200}-2^{200}\equiv0mod10\). Vậy \(12^{200}-2^{200}\) chia hết cho 10.
Chứng tỏ rằng số 2003200 - 2001200 chia hết cho 2 và 5
Chứng tỏ rằng biểu thức sau chia hết cho 10:
a)A=(11^200)-1 b)B=(12^300)-(2^300)
Sorry Nha Toán lớp 6
chứng tỏ rằng 162008-8200 chia hết cho 10
Ta có:
162008 - 8200
= (...6) - (84)50
= (...6) - (...6)50
= (...6) - (...6)
= (...0) chia hết cho 10
Đúng 0
Bình luận (0)
Ta có:
162008 - 8200
= (...6) - (84)50
= (...6) - (...6)50
= (...6) - (...6)
= (...0) chia hết cho 10
Đúng 0
Bình luận (0)
Cho A= 5+52+53+54+55+...5200
a)chứng tỏ rằng A chia hết cho 6
b)chứng tỏ rằng A chia cho 31 dư 30
a) A=5(1+5)+53(1+5)+...+5199(1+5)
=(1+5)(5+53+....+5199) chia hết cho 6
b) A:31 dư 30 hay A-30 chia hết cho 31
Ta có A=5(1+5+52)+54(1+5+52)+57(1+5+52)+.....+598(1+5+52)
31(5+54+57+...+599) chia hết cho 31. Nên A chia cho 31 không dư
Đúng 0
Bình luận (0)
5) Chứng tỏ 21^10-1 chia hết cho 200
\(21^2\equiv1\left(mod8\right)\Leftrightarrow21^{10}\equiv1^5=1\left(mod8\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod8\right)\\ \Leftrightarrow21^{10}-1⋮8\left(1\right)\\ 21^5\equiv1\left(mod25\right)\Leftrightarrow21^{10}\equiv1^2=1\left(mod25\right)\\ \Leftrightarrow21^{10}-1\equiv0\left(mod25\right)\\ \Leftrightarrow21^{10}-1⋮25\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow21^{10}-1⋮25\cdot8=200\)
Đúng 0
Bình luận (0)



















