a, Tính diện tích của các hình chữ nhật AMND và BCNM (hình bên) theo a,b và k.
b, Tính diện tích của hình chữ nhật ABCD (hình bên) theo hai cách
c, Hãy điền vào chỗ trống(...) để được đẳng thức đúng:
k(a+b) = .....+.....
Cho hình vẽ bên ,biết ABCD là hình chữ nhật có AB = 5cm;AD = 4cm,MN vuông góc với cạnh AB
Gọi độ dài của đoạn thẳng AM là a. Hãy viết các biểu thức tính chu vi và diện tích hình chữ nhật AMND theo a
Biểu thức tính: Chu vi hình chữ nhật AMND: (a+4) * 2
Diện tích hình chữ nhật AMND: a * 4
Tính diện tích hình chữ nhật ABCD ở hình bên theo hai cách, trong đó có cách tính tổng diện tích các hình chữ nhật AEFD và EBCF. Hai cách đó minh hoạ tính chất nào của phép nhân phân số?
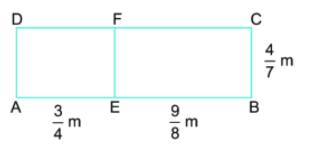
Cách 1:
Chiều dài hình chữ nhật ABCD là:
\(\dfrac{3}{4} + \dfrac{9}{8} = \dfrac{{15}}{8}\,(m)\)
Diện tích hình chữ nhật ABCD là:
\(\dfrac{4}{7}.\dfrac{{15}}{8} = \dfrac{{15}}{{14}}\) (m2)
Cách 2:
Diện tích hình chữ nhật ADFE là:
\(\dfrac{3}{4}.\dfrac{4}{7} = \dfrac{3}{7}\)(m2)
Diện tích hình chữ nhật BCFE là:
\(\dfrac{4}{7}.\dfrac{9}{8} = \dfrac{9}{{14}}\) (m2)
Diện tích hình chữ nhật ABCD là:
\(\dfrac{3}{7} + \dfrac{9}{{14}} = \dfrac{{15}}{{14}}\) (m2)
Hai cách trên minh họa tính chất phân phối của phép nhân đối với phép cộng: \((\dfrac{3}{4} + \dfrac{9}{8}). \dfrac{4}{7}=\dfrac{3}{4}.\dfrac{4}{7}+\dfrac{4}{7}.\dfrac{9}{8}\)
Cách 1:
Chiều dài hình chữ nhật ABCD là:
47.158=151447.158=1514 (m2)
Cách 2:
Diện tích hình chữ nhật ADFE là:
47.98=91447.98=914 (m2)
Diện tích hình chữ nhật ABCD là:
(34+98).47=34.47+47.98
Cho hình vẽ bên. Biết ABCD và BMNC là các hình vuông cạnh 8 cm. Viết tiếp vào chỗ chấm:
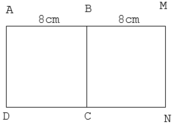
a) Đoạn thẳng AM vuông góc với các đoạn thẳng
b) Diện tích hình chữ nhật AMND
Tính diện tích của mảnh đất có kích thước theo hình vẽ bên (được tạo bởi hình chữ nhật ABCD và hình vuông CEMN)
Diện tích hình chữ nhật: \(14\times6=84\left(m^2\right)\)
Diện tích hình vuông: \(7\times7=49\left(m^2\right)\)
Diện tích mảnh đất: \(84+49=133\left(m^2\right)\)
Diện tích ABCD: 14 x 6= 84 m2
Diện tích CEMN: 7 x 7= 49 m2
Diện tích mảnh đất: 84 + 49= 133 m2
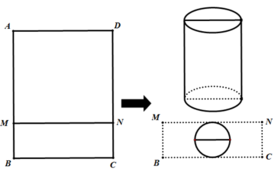
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 1 m 2 và cạnh BC = x(m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành hai hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM, phần hình chữ nhật BCNM được cắt một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
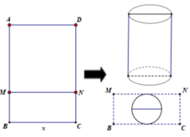
A. 1,37m
B. 1,02m
C. 0,97m
D. 1m
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 1m2 và cạnh BC=x(m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành hai hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM, phần hình chữ nhật BCNM được cắt một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).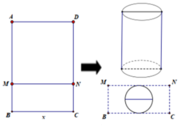
A. 1,37m
B. 1,02m
C. 0,97m
D. 1m
1. Cho hình thang ABCD có góc A và góc B vuông.Trên AB lấy điểm M,trên CD lấy điểm N sao cho MN song song với AD. Cho biết AM = 35cm, MB = 15cm, BC = 60cm và AD = 70cm. Tính diện tích của hình thang AMND ( giải chi tiết theo cấp tiểu học)
2. Một miếng bìa hình chữ nhật có chiều dài 16cm, chiều rộng 9cm. Người ta cắt miếng bìa (dọc theo chiều rộng để được hai phần, một phần hình vuông và một phần hình chữ nhật).
a) Tính chu vi và diện tích tấm bìa hình vuông.
b) Tính chu vi và diện tích tấm bìa hình chữ nhật.
1.  Ta có:
Ta có:
SNCP = SCPD - SNPD
= 10 x (15 + 35) : 2 - 10 x 35 : 2 = 75
RN = 75 x 2 : (15 + 35) = 3 (cm)
MN = 60 + 3 = 63 (cm)
SAMND = (63 + 70) x (15 + 35) : 2
= 2327,5
bn co the ve hinh cho mk dc ko. tai vi co mot so cho ki hieu bn them vao mk ko bit no o dau
Cho hình bên có các kích thước ghi trên hình .a Tính diện tích của các hình thang . b Tính tỉ số phần trăm diện tích của hình chữ nhật ABCD và diện tích hình thang .A và E 1 cm G và B 3 cm B và C 4 cmD và C 6 cm
Sử dụng mảnh inox hình chữ nhật ABCD có diện tích bằng 1 m 2 và cạnh BC= x (m) để làm một thùng đựng nước có đáy, không có nắp theo quy trình như sau: Chia hình chữ nhật ABCD thành 2 hình chữ nhật ADNM và BCNM, trong đó phần hình chữ nhật ADNM được gò thành phần xung quanh hình trụ có chiều cao bằng AM; phần hình chữ nhật BCNM được cắt ra một hình tròn để làm đáy của hình trụ trên (phần inox còn thừa được bỏ đi). Tính gần đúng giá trị x để thùng nước trên có thể tích lớn nhất (coi như các mép nối không đáng kể).
![]()
![]()
![]()