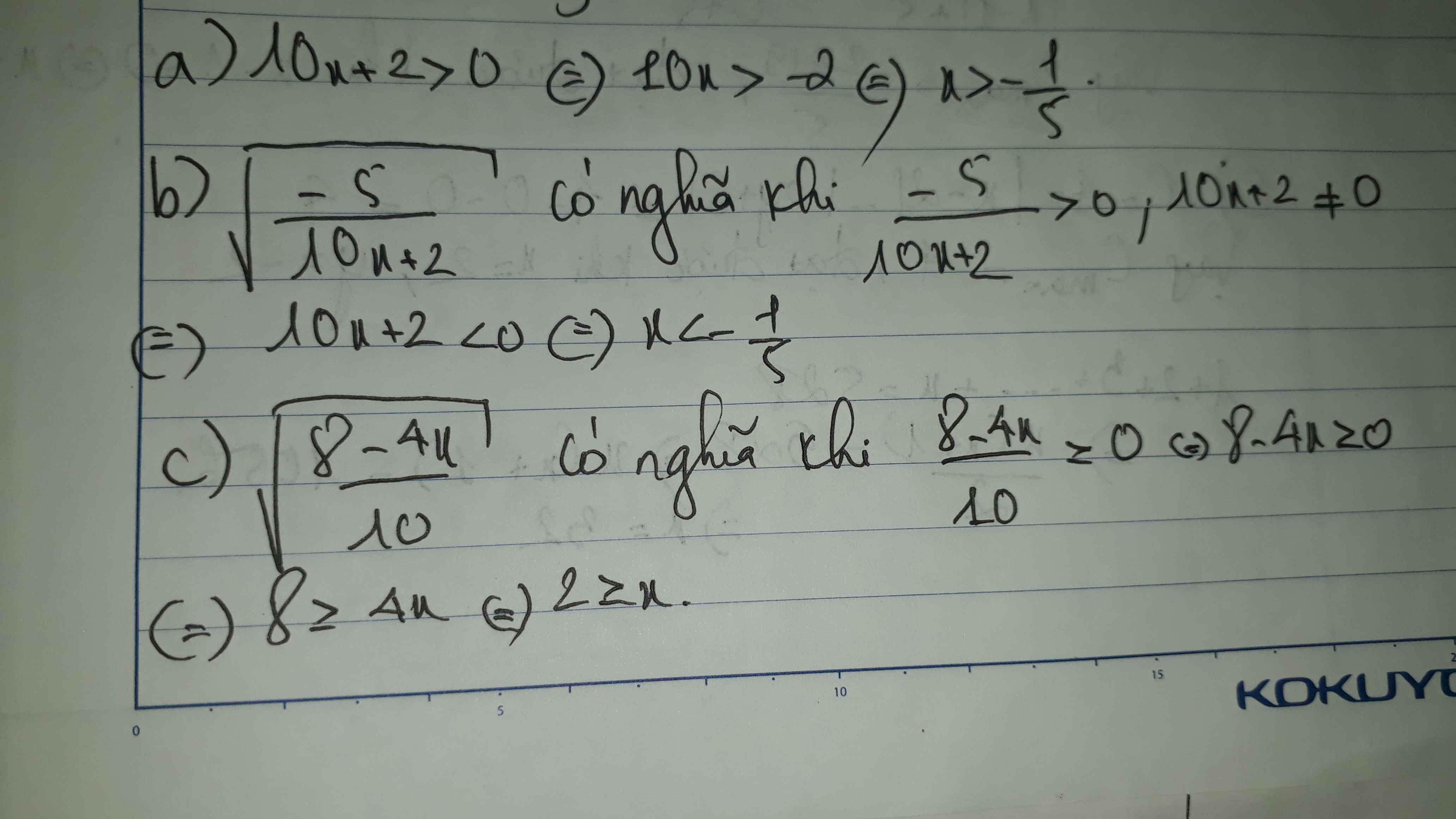\(A=x^4+4x^3+10x^2+12x=x^4+4x^2+9+4x^3+12x+6x^2-9\)

<=>\(A=x^4+4x^2+9+4x^3+12x+6x^2-9\)

<=>\(A=\left(x^2\right)^2+\left(2x\right)^2+3^2+2.x^2.2x+2.2x.3+2.x^2.3-9\)

<=>\(A=\left(x^2+2x+3\right)^2-9\)

<=>\(A=\left[\left(x+1\right)^2+2\right]^2-9\)

Vì \(\left(x+1\right)^2\ge0\Leftrightarrow\left(x+1\right)^2+2\ge2\Leftrightarrow\left[\left(x+1\right)^2+2\right]^2\ge4\)\(\Leftrightarrow A=\left[\left(x+1\right)^2+2\right]^2-9\ge-5\)

=>A_min=-5 <=> x=-1

Vậy A_min=5 tại x=-1

\(\frac{x}{3}=\frac{y}{4}\)

\(\Rightarrow4x=3y\)

\(\Rightarrow\frac{x}{y}=\frac{3}{4}\)

\(\Rightarrow\orbr{\begin{cases}x=3\\x=-3\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}y=4\\y=-4\end{cases}}\)

\(\frac{x}{3}=\frac{y}{4}\Rightarrow4x=3y\Rightarrow4x-3y=0\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{4x}{12}=\frac{3y}{12}=\frac{4x-3y}{12-12}=\frac{0}{0}\)

Sai chỗ nào nhỉ,mình cho 3 .

Ta có Từ (1)<=>7x-4x<8+4

                   <=>3x<12

                    <=>x<4 (3)

Từ (2) <=> 10x-12x >-8-15

           <=>-2x > -23

           <=>x > -11,5(4)

Từ (3), (4) suy ra -11.5<x<4 mà x >0 nên 0<x<4

a) Ta có: A = 0

=> x² + 2x - 3 = 0

=> x² + 3x - x - 3 = 0

=> x(x + 3) - (x + 3) = 0

=> (x - 1)(x + 3) = 0

=> \(\orbr{\begin{cases}x-1=0\\x+3=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)

Vậy ...

b) Ta có: B = 0

=> -3x² + 12x - 9 = 0

=> -3x² + 3x + 9x - 9 = 0

=> -3x(x - 1) + 9(x - 1) = 0

=> (-3x + 9)(x - 1) = 0

=> -3(x - 3)(x - 1) = 0

=> (x - 3)(x - 1) = 0

=> \(\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\)

=> \(\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

Vậy ...

c) C = 0

=>  10x² - 7x - 3 = 0

=> 10x² - 10x + 3x - 3 = 0

=> 10x(x - 1) + 3(x - 1) = 0

=> (10x  + 3)(x - 1) = 0

=> \(\orbr{\begin{cases}10x+3=0\\x-1=0\end{cases}}\)

=> \(\orbr{\begin{cases}10x=-3\\x=1\end{cases}}\)

=> \(\orbr{\begin{cases}x=-\frac{3}{10}\\x=1\end{cases}}\)

d) D = 0

=> -7x⁴ + 10x³ - 3x² = 0

=> x²(-7x² + 10x - 3) = 0

=> x²(-7x² + 7x + 3x - 3) = 0

=> x².[-7x(x - 1) + 3(x - 1)] = 0

=> x².(-7x + 3)(x - 1) = 0

=> x^2 = 0

-7x + 3 = 0

hoặc  x - 1 = 0

=> x=  0

-7x = -3

hoặc x = 1

=> x = 0

hoặc x = 3/7

hoặc x = 1

Vậy ...

a) \(A=x^2+2x-3\)

\(x^2+2x-3=0\)

\(\Leftrightarrow\left(x-1\right)\left(x+3\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\x+3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=1\\x=-3\end{cases}}\)

b) \(B=-3x^2+12x-9\)

\(-3x^2+12x-9=0\)

\(\Leftrightarrow-3\left(x^2-4x+3\right)=0\)

\(\Leftrightarrow-3\left(x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}x-3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=3\\x=1\end{cases}}\)

c) \(C=10x^2-7x-3\)

\(10x^2-7x-3=0\)

\(\Leftrightarrow x\left(10x+3\right)-\left(10x+3\right)=0\)

\(\Leftrightarrow\left(10x+3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\orbr{\begin{cases}10x+3=0\\x-1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-\frac{3}{10}\\x=1\end{cases}}\)

\(\Rightarrow\orbr{\begin{cases}x=-\frac{3}{10}\\x=1\end{cases}}\)

d) \(D=-7x^4+10x^3-3x^2\)

\(-7x^4+10x^3-3x^2=0\)

\(\Leftrightarrow-x^2\left(7x^2-10x+3\right)=0\)

\(\Leftrightarrow-x^2\left(7x^2-3x-7x+3\right)=0\)

\(\Leftrightarrow-x^2\left[x\left(7x-3\right)-\left(7x-3\right)\right]=0\)

\(\Leftrightarrow-x^2\left(7x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow x^2\left(7x-3\right)\left(x-1\right)=0\)

\(\Leftrightarrow\hept{\begin{cases}x^2=0\\7x-3=0\\x-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=0\\x=\frac{3}{7}\\x=1\end{cases}}\)(thay ngoặc nhọn bằng ngoặc vuông nhé, phần kl cũng thay luôn như thế nhé)

\(\Rightarrow\hept{\begin{cases}x=0\\x=\frac{3}{7}\\x=1\end{cases}}\)

\(\Leftrightarrow x^4-4x^3+12x^2-32x+32=\left(y-5\right)^2\)

\(\Leftrightarrow\left(x-2\right)^2\left(x^2+8\right)=\left(y-5\right)^2\)

- Với \(x=2\Rightarrow y=5\)

- Với \(x\ne2\Rightarrow x-2\) là ước của \(y-5\) 

Đặt \(y-5=n\left(x-2\right)\)

\(\Rightarrow\left(x-2\right)^2\left(x^2+8\right)=n^2\left(x-2\right)^2\)

\(\Rightarrow x^2+8=n^2\)

\(\Rightarrow\left(n-x\right)\left(n+x\right)=8\)

\(\Rightarrow\left[{}\begin{matrix}x=1;n=-3\Rightarrow y=8\\x=-1;n=-3\Rightarrow y=14\\x=1;n=3\Rightarrow y=2\\x=-1;n=3\Rightarrow y=-4\end{matrix}\right.\) 

cứu mị :<

làm khuyến mại 1 câu;

a) = 12x² -12x² +20x -10x +17 =0

10x = -17

x = -17/10

x/2 - ( 3x/5 - 13/5 ) = -( 7/5 + 7/10x )

a) = 12x2 -12x2 +20x -10x +17 =0

10x = -17

x = -17/10

a) 5.(x^2-3x+1)+x.(1-5x)=x-2

\(\Leftrightarrow5x^2-15x+5+x-5x^2=x-2\)

\(\Leftrightarrow-14x-x=-2-5\)

\(\Leftrightarrow-15x=-7\)

\(\Leftrightarrow x=\frac{7}{15}\)

b\(,3x.\left(\frac{4}{3}+1\right)-4x\left(x-2\right)=10\)

\(\Leftrightarrow4x+3x-4x^2+8x-10=0\)

\(\Leftrightarrow-4x^2+15x-10=0\)

Đề sai???

\(c,12x^2-4x\left(3x-5\right)=10x-17\)

\(\Leftrightarrow12x^2-12x^2+20x-10x=-17\)

\(\Leftrightarrow10x=-17\)

\(\Leftrightarrow x=-\frac{17}{10}\)

\(d,4x\left(x-5\right)-7x\left(x-4\right)+3x^2=12\)

\(\Leftrightarrow4x^2-20x-7x^2+28x+3x^2=12\)

\(\Leftrightarrow8x=12\)

\(\Leftrightarrow x=\frac{3}{2}\)

\(12x^2-2x-10x^3=0\)

\(\Rightarrow2x\left(6x-1-5x^2\right)=0\)

\(\Rightarrow2x\left(-5x^2+6x-1\right)=0\)

\(\Rightarrow2x\left(-5x^2+5x+x-1\right)=0\)

\(\Rightarrow2x\left[5x\left(x-1\right)+\left(x-1\right)\right]=0\)

\(\Rightarrow2x\left(x-1\right)\left(5x+1\right)=0\)

* 2x = 0 => x = 0

* x - 1 = 0 => x =1

* 5x + 1 = 0 => x = - 0,2

Vậy.....