Kẻ trung tuyến AM 

TAm giác ABC có AM là trung tuyến 

=> AM = MC=1/2 BC

TAm giác AMC có AM =MC và C = 60 độ => tam giác AMC đều

=> AC  = AM = 1

ta lại có AM = 1/2 BC => BC= 2AM = 2.1 = 2 

TAm giác ABC vuông tại A , theo py ta go

                           AB^2 + AC^2 = BC ^2

                =>   AB ^2 = BC^2  - AC^2

              = >   AB^2   = 2^2 - 1^2 

                                 =  4 - 1 = 3

               =>AB  = căn 3 

Bạn xem lại đề đi

đề đúng đó

Cách 3: (Lớp 8) Trên nửa mặt phẳng bờ AC không chứa B, dựng tam giác đều ACG.

Có ngay AB = AC = AG và ^BAG = ^BAC + ^CAG = 90⁰ => \(\Delta\)BAG vuông cân tại A

Suy ra ^CBG = ^ABC - ^ABG = 30⁰ = ^DAB      (1)

Cũng dễ thấy ^ADB = 135⁰; ^BCG = ^ACB + ^ACG = 135⁰ => ^BCG = ^ADB (2)

Từ (1) và (2) suy ra \(\Delta\)CGB ~ \(\Delta\)DBA (g.g). Từ đây \(\frac{AD}{BC}=\frac{AB}{BG}=\frac{1}{\sqrt{2}}\)

Vậy \(AD=\frac{BC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)(cm).

Trên nửa mặt phẳng bờ BC chứa A dựng \(\Delta\)BCE vuông cân tại E

Khi đó ^EBA = ^ABC - ^EBC = 30⁰ = ^DAB

\(\Delta\)AEC = \(\Delta\)AEB (c.c.c) => ^EAB = ^BAC/2 = 15⁰ = ^DBA

Xét \(\Delta\)BEA và \(\Delta\)ADB có: AB chung, ^EAB = ^DBA, ^EBA = ^DAB

=> \(\Delta\)BEA = \(\Delta\)ADB (g.c.g) => AD = BE = \(\frac{BC}{\sqrt{2}}=\frac{2}{\sqrt{2}}=\sqrt{2}\)(cm).

Cách 2: Trên nửa mặt phẳng bờ AC không chứa B dựng \(\Delta\)ADF vuông cân tại D.

Có ^BDF = 360⁰ - 90⁰ - ^ADB = 135⁰ = ^BDA. Do đó \(\Delta\)DAB = \(\Delta\)DFB (c.g.c)

=> ^ABF = 2.^ABD = 30⁰ = ^BAC. Kết hợp với BF = AB = AC suy ra \(\Delta\)BAF = \(\Delta\)ABC (c.g.c)

=> AF = BC hay \(AD\sqrt{2}=BC=2\). Vậy nên \(AD=\frac{2}{\sqrt{2}}=\sqrt{2}\)(cm).

Kẻ đường cao BH (H thuộc AC)

Do góc A nhọn \(\Rightarrow\) H nằm giữa A và C

Ta có: \(S_{ABC}=\dfrac{1}{2}BH.AC\Leftrightarrow\dfrac{2}{5}bc=\dfrac{1}{2}BH.b\)

\(\Rightarrow BH=\dfrac{4c}{5}\)

Áp dụng Pitago cho tam giác vuông ABH:

\(AH^2=AB^2-BH^2=c^2-\left(\dfrac{4c}{5}\right)^2=\dfrac{9c^2}{25}\Rightarrow AH=\dfrac{3c}{5}\)

\(\Rightarrow CH=AC-AH=b-\dfrac{3c}{5}\)

Pitago tam giác vuông BCH:

\(BC=\sqrt{BH^2+CH^2}=\sqrt{\left(\dfrac{4c}{5}\right)^2+\left(b-\dfrac{3c}{5}\right)^2}=\sqrt{b^2-\dfrac{6}{5}bc+c^2}\)

                         75% = 3/4

Tổng độ dài AB và AC là: 3 + 4  = 7 (phần)

Giá trị 1 phần: 120 : ( 3 + 4 + 5) = 10 (cm)

Cạnh AC: 10 x 3 = 30 (cm)

Cạnh AB: 10 x 4 = 40 (cm)

Cạnh BC: 10 x 5 = 50 ( cm)

DT tam giác ABC:( 30 x 40): 2= 60 (cm2)

Chiều cao tương ứng của cạnh BC: 60 x 2 : 50 = 24

Học Tốt ^-^

-Áp dụng định lí: Trong một tam giác vuông, đoạn thẳng đối diện với góc 30^o thì bằng  \(\frac{1}{2}\)cạnh huyền

=> \(AB=\frac{1}{2}.BC\)=> BC = 2. AB = 2. 3 = 6 (cm)

-Tam giác ABC vuông tại A, theo định lí Pytago, ta có:

BC² = AB² + AC²

=> 6² = 3² + AC²

=> AC² =  36 - 9 = 27 

=> \(AC=\sqrt{27}\)  (cm)

Ta có: AC^2 = AB^2 +BC^2 - 2AB.BC.cos(ABC) 
<=> 14^2 = 16^2 +BC^2 -2.16.BC.cos(60) 
<=> BC^2 - 16BC + 60 = 0 
<=> BC = 6 hoặc BC=10 
Với BC=6 hoặc BC=10 đều thỏa mãn tổng 2 cạnh lớn hơn 1 cạnh 
Vậy BC=6 hoặc BC=10

trong một tg nhọn thì bình phương một cạnh bất kì bằng tổng bình phương cạnh thứ 2 và bình phương cạnh thứ 3 trừ cho 2. cạnh 2 .cạnh 3 . cos góc tạo bởi cạnh 2 và cạnh 3 
cho tg nhọn ABC có cạnh AB=c AC=b BC=a kẻ đường cao BH 
ta có HC^2= (AC-AH)^2 <=> BH^2 + HC^2 = AC^2 + AB^2 - 2AB.AC.AH/AB 
<=> a^2=b^2+c^2-2bc.cosBAC => đpcm

như nnafy hả

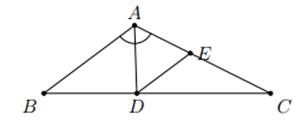
\(\text{Đặt AD=DE=EA=x. Ta có}\)

\(\text{Đặt AD=DE=EA=x. Ta có:}\)

\(\dfrac{DE}{AB}=\dfrac{CE}{CA}=\dfrac{x}{3}=\dfrac{6-x}{6}\)

\(\Rightarrow x=2\). \(\text{Vậy}\) \(AD=2cm\)

Bài toán này ở chương trình lớp 10,11, bạn xem lại đề

quan trọng là phải làm đc bài, ko cần bt nó ở lớp mấy đou nhé