Cho tam giác ABC vuông tại A, AB < AC, vẽ AH vuông góc với BC ( H thuộc BC )
a) So sánh góc B và góc C, BH và CH
b) Gọi M là giao điểm của BC. Chứng minh AH < MC
Ai đang onlice thì giúp mình với mình cần gấp lắm
Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC (H thuộc AC) , kẻ CK vuông góc với AB (K thuộc BC) .
a) Chứng minh AH=AK.
b) Gọi I là giao điểm của BH và CK. Chứng minh AI là đường trung trực của HK.
c) Kẻ Bx vuông góc với AB tại B, gọi E là giao điểm của Bx với AC. Chứng minh BC là phân giác của góc HBE.
d) So sánh CH với CE
Hình tự vẽ nha bạn
a) Xét \(\Delta AHB\)và \(\Delta AKC\)có:
\(\hept{\begin{cases}\widehat{A}:chung\\AB=AC\left(gt\right)\\\widehat{AHB}=\widehat{AKC}\left(gt\right)\end{cases}}\)
\(\Rightarrow\Delta AHB=\Delta AKC\left(ch-gn\right)\)
=>AH=AK ( 2 cạnh tương ứng) -đpcm
b) Xét \(\Delta AKI\)và \(\Delta AHI\)có:
\(\hept{\begin{cases}AK=AH\\\widehat{AKI}=\widehat{AHI}\\AI:chung\end{cases}}\)
\(\Rightarrow\Delta AKI=\Delta AHI\left(ch-cgv\right)\)
\(\Rightarrow\widehat{IAK}=\widehat{IAH}\)( 2 góc tương ứng)
=> AI là ti phân giác góc KAH
Xét \(\Delta KAH\)cân tại A ( do AH=AK ) có AI là tia phân giác ứng cạnh KH
=> AI đồng thời là đường trung trực của cạnh KH (t/c) -đpcm
c) Kẻ CM \(\perp\)BE
Xét tứ giác BKCM có:
\(\hept{\begin{cases}\widehat{CKB}=90^0\\\widehat{KBM}=90^0\\\widehat{BMC}=90^0\end{cases}}\)
=> tứ giác BKCM là hình chữ nhật (dấu hiệu nhận biết)
=> BK=CM (t/c) (1)
Dễ dàng chứng minh đc: BK=CH (2)
Từ (1) và (2) có : CM=CH
Xét \(\Delta BHC\)và \(\Delta BMC\)có:
\(\hept{\begin{cases}CH=CM\\\widehat{BHC}=\widehat{BMC}\\CB:chung\end{cases}}\)
=> \(\Delta BHC=BMC\left(ch-cgv\right)\)
=> \(\widehat{CBH}=\widehat{CBM}\)(2 góc tương ứng)
=> BC là tia phân giác góc HBM
hay BC là tia phân giác HBE -đpcm
Chúc bạn học tốt!
d) Xét tam giác CME vuông tại M có CE là cạnh huyền
=>CE>CM (trong tam giác vuông cạnh huyền là cạnh lớn nhất)
mà CH=CM do \(\Delta CBH=\Delta CBM\)
=>CE>CH
Tam giác ABC có góc B>góc C, gọi AH là đường vuông góc kẻ từ điểm A đến BC (H thuộc BC), M là điểm thuộc đoạn AH
a) So sánh: BH và CH
b) So sánh: MB và MC
c) Chứng minh rằng: AH< AB+AC:2
hung huyen ngu vai
Cho tam giác nhọn có AB<AC;AH vuông góc với BC( H thuộc BC ). a) So sánh HB với CH; AB với AH. So sánh BH với AB+AC với BC. Kẻ BC vuông góc với AC ( K thuộc AC). Gọi I là giao điểm của AH và BK. Chứng minh CI vuông góc với AB
Cho tam giác nhọn có AB<AC;AH vuông góc với BC( H thuộc BC )
a) So sánh HB với CH; AB với AH. So sánh BH với AB+AC với BC.
b) Kẻ BC vuông góc với AC ( K thuộc AC). Gọi I là giao điểm của AH và BK. Chứng minh CI vuông góc với AB
cho tam giác ABC cân tại A. kẻ AH vuông góc với BC(h thuộc bc). Gọi N là trung điểm của AC
a) So sánh AB và AH
b)Gọi G là giao điểm của AH và BN,M là trung diểm của AB
chứng minh: MC=NB
c)Trên tia đối của tia NB lấy diểm K sao cho NK=NG. CHứng minh AG=CK, từ đó suy ra BC +AG>4MG
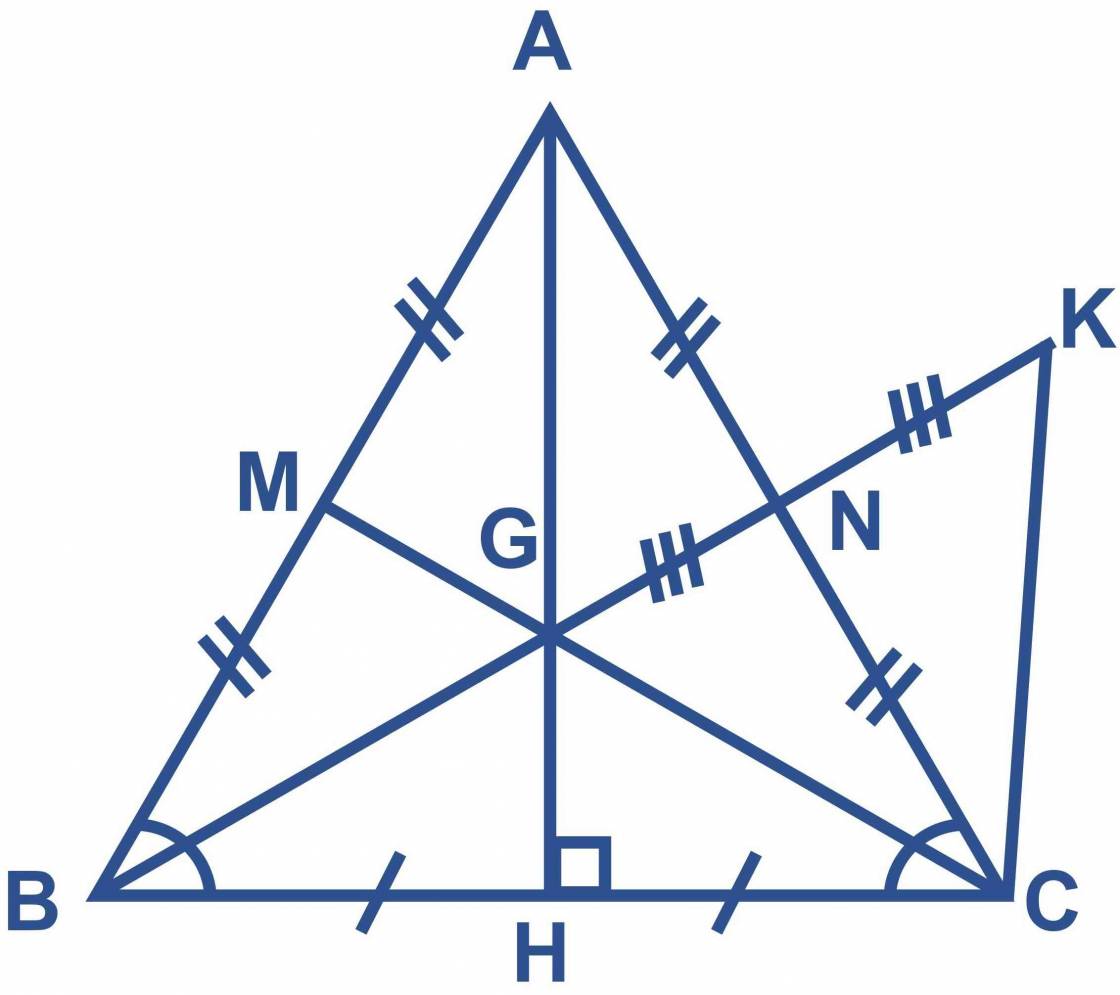
a) trong ΔABC, có góc AHB là góc vuông
góc ABH là góc nhọn
⇒ góc AHB > góc ABH
⇒ AB > AH
b) M là trung điểm của AB và N là trung điểm của AC, mà AB = AC (2 cạnh bên của tam giác cân) ⇒ MB = NC
xét tam giác MBC và tam giác NCB, ta có :
MB = NC (cmt)
góc B = góc C (2 góc đáy của 1 tam giác cân)
BC là cạnh chung
⇒ tam giác MBC = tam giác NCB (c-g-c)
⇒ MC = NB (2 cạnh tương ứng)
c) xét tam giác NAG và tam giác NCK , ta có :
NA = NC (vì N là trung điểm của cạnh AC)
góc NAG = góc NCK (đối đỉnh)
NG = NK (gt)
=> tam giác NAG = tam giác NCK (c-g-c)
=> AG = CK (2 cạnh tương ứng)
1.Cho tam giác ABC có AB=3cm,AC=4cm,BC=5cm
a) Chứng tỏ tam giác ABC vuông tại A.
b) Trên tia đối của tia AC lấy điểm D sao cho CD=6cm.Tính độ dài đoạn thẳng BD.
2.Cho tam giác ABC, biết AB = 12cm,AC = 9cm,BC = 15cm.
a) Chứng tỏ tam giác ABC vuông.
b) Kẻ AH vuông góc với BC tại H, biết AH = 7,2cm.Tính độ dài đoạn thẳng BH và HC.
3.Cho tam giác nhọn ABC(AB<AC). Kẻ AH vuông góc với BC tại H. Tính chu vi tam giác ABC biết AC = 20cm, AH = 12cm, BH = 5cm.
4.Cho tam giác ABC cân tại A, kẻ AH vuông góc với BC
a) Chứng minh tam giác AHB = tam giác AHC
b) Từ H kẻ HM vuông góc với AB tại M. Trên cạnh AC lấy điểm N sao cho BM = CN. Chứng minh HN vuông góc AC.
5.Cho tam giác ABC cân tại A, tia phân giác của góc A cắt BC tại I
a) Chứng minh tam giác AIB = tam giác AIC
b) Lấy M là trung điểm AC. Trên tia đối của tia MB lấy điểm D sao cho MB = MD. Chứng minh AD song song BC và AI vuông góc AD.
c) Vẽ AH vuông góc BD tại H, vẽ CK vuông góc BD tại K. Chứng minh BH = DK.
6.Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc BD(E thuộc BD). AE cắt BC ở K.
a) Chứng minh tam giác ABE = tam giác KBE và suy ra tam giác BAK cân.
b) Chứng minh tam giác ABD = tam giác KBD và DK vuông góc BC.
c) Kẻ AH vuông góc BC(H thuộc BC). Chứng minh AK là tia phân giác của HAC.
Mọi người vẽ hình lun 6 bài giúp mình nha! Mình đang cần gấp!:(
Ai đó giúp mình với! Mình đang cần gấp!:( Các bạn vẽ hình lun giúp mình nha! Cảm ơn các bạn nhìu!:)
Do tam giác ABC có
AB = 3 , AC = 4 , BC = 5
Suy ra ta được
(3*3)+(4*4)=5*5 ( định lý pi ta go)
9 + 16 = 25
Theo định lý py ta go thì tam giác abc vuông tại A
a) Áp dụng định lý Pytago vào \(\Delta\)ABC có
AB2+AC2=BC2
thay AB=3cm, AC=4cm va BC=5cm, ta có:
32+42=52
=> 9+16=25 (luôn đúng)
=> đpcm
b) có D nằm trên tia đối của tia AC
=> D,A,C thằng hàng và A nằm giữa D và C
=> DA+AC=DC
=> DA+4=6
=>DA=2(cm)
áp dụng định lý Pytago vào tam giác ABD vuông tại A có:
AB2+AD2=BD2
=> 32+22=BD2
=> 9+4=BD2
=> \(BD=\sqrt{13}\)(cm)
Cho tam giác ABC cân tại A vẽ BH vuông góc với AC ; CK vuông góc với AB a) vẽ hình b) chứng minh AH = AK c) gọi I là giao điểm của BH và CK . Chứng minh Góc KAI = góc HAI d) AI cắt BC tại P . Chứng minh AI vuông góc BC tại P
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc A chung
=>ΔAHB đồng dạng với ΔAKC
=>AH=AK
c: Xet ΔAKI vuông tại K và ΔAHI vuông tại H có
AI chung
AK=AH
=>ΔAKI=ΔAHI
=>góc KAI=góc HAI
d: ΔABC cân tại A
mà AP là phân giác
nên P là trung điểm của BC
=>AP vuông góc BC
Câu 4: (4,5 điểm) Cho ABC có AB = 6cm, AC = 8cm, BC = 10.
a) Chứng minh ABC là tam giác vuông.
b) So sánh các góc của ABC.
c) Kẻ AH vuông góc với BC (H thuộc BC). So sánh AH, BH, CH.
d) Lấy điểm M trên cạnh BC sao cho H là trung điểm của BC. Chứng minh ABM là tam giác cân.
e) Gọi N là trung điểm của AM (N thuộc AM), gọi G là điểm thuộc đoạn AH sao cho ag=2gh. chứng minh 3 điểm b ; g ; n thẳng hàng
Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC, kẻ CK vuông góc với AB
a) Chứng minh AH= AK
b) Gọi I là giao điểm của BH và CK. Chứng minh AI là trung trực của HK
c) Kẻ Bx vuông góc với AB tại B, gọi E là giao điểm của Bx với AC. Chứng minh BC là phân giác của HBE
d) So sánh CH với CE
Mình đã làm đc câu a, b nhờ các bạn giúp câu c, d nhé
Mình đang cân gấp!!!
Câu 4: (4,5 điểm) Cho ABC có AB = 6cm, AC = 8cm, BC = 10.
a) Chứng minh ABC là tam giác vuông.
b) So sánh các góc của ABC.
c) Kẻ AH vuông góc với BC (H thuộc BC). So sánh AH, BH, CH.
d) Lấy điểm M trên cạnh BC sao cho H là trung điểm của BC. Chứng minh ABM là tam giác cân.
e) Gọi N là trung điểm của AM (N thuộc AM), gọi G là điểm thuộc đoạn AH sao cho ag=2gh. chứng minh 3 điểm b ; g ; n thẳng hàng