Cho tam giác ABC cân tại A kẻ các đường cao BD và CE tứ giác BECD là hình gì vì sao ( giup em voi )

Những câu hỏi liên quan
Cho tam giác ABC cân tại A kẻ các đường cao BD và CE tứ giác BECD là hình gì vì sao
Xem chi tiết
Hình Thang cân
Ta có: tam giác ABC là tam giác cân tại A.
=> góc B= góc C
Vì BD và CE là phân giác góc B và C
=> góc DBC = góc EBD = góc DCE = góc ECB
Xét tam giác EBC và tam giác DBC có:
góc ECB = góc DBC
góc BCD = góc EBC
Chung cạnh BC
Hình thang cân nhé, c/m tam giác ADB~AEC (g.g) -> AE/AC=AD/AB -> tgADE~tgABC (c.g.c). Do đó góc ADE= góc ABC, mà ABC=ACB (gt) --> góc ADE=ACB --> DE//BC--> BEDC là hình thang. Mà nó lại có 2 góc đáy = nhau--> đpcm
Cho ABC cân tại A . Kẻ các đường cao BD CE , . Tứ giác BEDC là hình gì? Vì sao?
Xét ΔABD vuông tại D và ΔACE vuông tại E có
AB=AC
\(\widehat{A}\) chung
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AD}{AC}\)
Do đó: ED//BC
Xét tứ giác BEDC có ED//BC
nên BEDC là hình thang
mà EC=BD
nên BEDC là hình thang cân
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A,đường trung tuyến BD và CE a) BD=CE b) Tứ giác BCDE là hình gì? c) kẻ đường cao AH của tam giác ABC .chứng minh BHDE là hình bình hành
Mong các bạn giúp đỡ
a) Ta có :
\(AB=AC\) (Δ ABC cân tại A)
\(\Rightarrow AE+BE=AD+DC\)
mà \(AE=BE\) (CE là trung tuyến nên E là trung điểm AB)
\(AD=DC\) (BD là trung tuyến nên D là trung điểm AC)
\(\Rightarrow AE=AD\)
Xét Δ ABD và Δ ACE có :
\(AB=AC\) (Δ ABC cân tại A)
Góc A chung
\(AE=AD\left(cmt\right)\)
⇒ Δ ABD = Δ ACE (góc, cạnh, góc)
\(\Rightarrow BD=CE\)
b) Xét tứ giác BCDE có :
\(\widehat{EBC}=\widehat{DCB}\) (Δ ABC cân tại A nên \(\widehat{ABC}=\widehat{ACB}\))
\(BD=CE\left(cmt\right)\)
⇒ Tứ giác BCDE là hình thang cân
c) Ta có :
CE là trung tuyến Δ ABC
BD là trung tuyến Δ ABC
⇒ ED là đường trung bình Δ ABC
\(\Rightarrow ED=\dfrac{1}{2}BC\)
mà H là trung điểm BC (Δ ABC cân tại A nên AH vừa là đường cao và trung tuyến)
\(\Rightarrow ED=BH\)
Xét tứ giác BHDE có :
ED song song BH (BCDE là hình thang cân nên ED song song BC)
\(ED=BH\left(cmt\right)\)
⇒ Tứ giác BHDE là hình bình hành.
Đúng 2
Bình luận (0)
help me///
1Hình thang ABCD có: AB//CD AB<CD kẻ đường cao AH,BK
a, CM: HD=KC <mk làm r nha>
b, biết AB=6cm, CD= 15cm.Tính độ dài AD,KC
2 ∆ABC cân tại A . phân giác BD và CE
a, Tứ giác BECD là hình gì ? vì sao?
b, CM: BE=ED=DC
c, biết Â=50* .tính các góc của tứ giác BECD
Cho tam giác ABC cân tại A, đường cao AM. Các đường trung tuyến BD, CE cắt nhau tại G. H, K thứ tự là trung điểm của BG, CG.
a) Tứ giác EHKD là hình gì? Vì sao?
b) Cho SABC = S36cm2. Tính SEHKD
cho tam giác ABC cân tại A các đường phân giác BD vá CE
a,tứ giác BE và DC là hình gì vì sao?
b,tính chu vi hình tứ giác BE và DC biết BC=15cm;DE=9cm
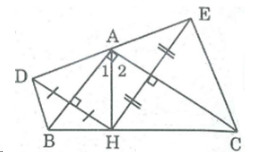
Cho tam giác ABC vuông tại A, đường cao AH. Gọi
b. Tam giác DHE là tam giác gì ? Vì sao ?
c. Tứ giác BDEC là hình gì ? Vì sao ?
d. Chứng minh rằng BC = BD + CE.
Tk:
a) Điểm D đối xứng điểm H qua trục AB
⇒ AB là đường trung trực của HD
⇒ AH = AD (tính chất đường trung trực) ⇒ ∆ ADH cân tại A
Suy ra: AB là tia phân giác của ˆDAH⇒ˆDAB=ˆA1DAH^⇒DAB^=A^1
Điểm H và điểm E đối xứng qua trục AC
⇒ AC là đường trung trực của HE
⇒ AH = AE (tính chất đường trung trực) ⇒ ∆ AHE cân tại A
Suy ra: AC là đường phân giác của ˆHAE⇒ˆA2=ˆEACHAE^⇒A^2=EAC^
Ta có: ˆDAE=ˆDAH+ˆHAEDAE^=DAH^+HAE^=2(ˆA1+ˆA2)=2.900=1800=2(A^1+A^2)=2.900=1800
Suy ra D, A, E thẳng hàng
Lại có: AD = AE (vì cùng bằng AH)
Nên điểm A là trung điểm của đoạn DE
Vậy điểm D đối xứng với điểm E qua điểm A.
b) Tam giác DHE có HA là trung tuyến và
Đúng 2
Bình luận (1)
Cho tam giác ABC cân tại A, kẻ các đường cao BD và CE
a/ cm Tam giác AEC = tam giác ADB
b/ cm tứ giác BDRC là hình thang cân
a: Xét ΔAEC vuông tại E và ΔADB vuông tại D có
AB=AC
góc A chung
Do đó: ΔAEC=ΔADB
b: Xét ΔABC có AE/AB=AD/AC
nên ED//BC
=>BEDC là hình thang
mà góc EBC=góc DCB
nên BEDC là hình thang cân
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường trung tuyến BD và CE cắt nhau tại M. Gọi H là trung điểm của MB và K là trung điểm của MC.
a) Tứ giác DEHK là hình gì? Vì sao?
b) Tam giác ABC có thêm điều kiện gì thì tứ giác DEHK là hình chữ nhật?
c) Nếu các đường trung tuyến BD và CE vuông góc với nhau thì tứ giác DEHK là hình gì? Vì sao?