Cho Δ ABC,gọi I là giao điểm các tia phân giác trong của góc B và góc C.Từ I kẻ IM ⊥ AB;IN ⊥ BC.Từ A kẻ đoạn thẳng song song với MN cắt BC tại P. C/m: MNPA là hình thang cân.

Những câu hỏi liên quan
Cho tam giác ABC nhọn có AB < AC . Gọi I là giao điểm tia phân giác của góc B và góc C . Từ I lần lượt kẻ các đường thẳng vuông góc với BC , AB , AC tại M , N , P . Chứng minh :
a, BM = BP
b, IM = IN
c, BP + CN = BC
d, AI là tia phân giác của góc BAC
Sửa đề: Vuông góc với AC,AP tại N,P
a: Xét ΔBPI vuông tại P và ΔBMI vuông tại M có
BI chung
\(\widehat{PBI}=\widehat{MBI}\)
Do đó: ΔBPI=ΔBMI
=>BP=BM
b: Xét ΔIMC vuông tại M và ΔINC vuông tại N có
CI chung
\(\widehat{MCI}=\widehat{NCI}\)
Do đó: ΔIMC=ΔINC
=>IM=IN
c: ΔMCI=ΔNCI
=>MC=CN
BP+CN
=BM+MC
=BC
d: ΔBPI=ΔBMI
=>IP=IM
mà IM=IN
nên IP=IN
Xét ΔAPI vuông tại P và ΔANI vuông tại N có
AI chung
IP=IN
Do đó: ΔAPI=ΔANI
=>\(\widehat{PAI}=\widehat{NAI}\)
=>AI là phân giác của \(\widehat{BAC}\)
Đúng 0
Bình luận (0)
Cho Δ ABC vuông tại A có góc B=300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông góc với BC (H ϵ BC).
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều.
b) Khi AB = 5cm. Tính BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
Help mik các bạn ơi, please!
Các bạn ơi, giúp mik bài này với!Cho Δ ABC vuông tại A có góc B 300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông với BC (HϵBC)a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đềub) Khi AB 5cm. Tính độ dài BC, ACc) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH(Các bạn vẽ luôn hộ mik hình nha, ko vẽ cũng đc)Thanks các bạn nhiều!
Đọc tiếp
Các bạn ơi, giúp mik bài này với!
Cho Δ ABC vuông tại A có góc B = 300. Tia phân giác góc C cắt AB tại D. Kẻ DH vuông với BC (HϵBC)
a) C/m Δ BCD là tam giác cân và Δ ACH là tam giác đều
b) Khi AB = 5cm. Tính độ dài BC, AC
c) Gọi I là giao điểm của HD và AC. C/m Δ IBC là tam giác đều và IC // với AH
(Các bạn vẽ luôn hộ mik hình nha, ko vẽ cũng đc)
Thanks các bạn nhiều!
a) Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{ABC}+\widehat{ACB}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{ACB}=90^0-\widehat{ABC}=90^0-30^0=60^0\)
Ta có: CD là tia phân giác của \(\widehat{ACB}\)(gt)
nên \(\widehat{DCB}=\dfrac{\widehat{ACB}}{2}=\dfrac{60^0}{2}=30^0\)
mà \(\widehat{DBC}=30^0\)(gt)
nên \(\widehat{DBC}=\widehat{DCB}\)
Xét ΔBCD có \(\widehat{DBC}=\widehat{DCB}\)(cmt)
nên ΔBCD cân tại D(Định lí đảo của tam giác cân)
Xét ΔACD vuông tại A và ΔHCD vuông tại H có
CD chung
\(\widehat{ACD}=\widehat{HCD}\)(CD là tia phân giác của \(\widehat{ACH}\))
Do đó: ΔACD=ΔHCD(Cạnh huyền-góc nhọn)
Suy ra: CA=CH(hai cạnh tương ứng)
Xét ΔCAH có CA=CH(cmt)
nên ΔCAH cân tại C(Định nghĩa tam giác cân)
Xét ΔCHA cân tại C có \(\widehat{ACH}=60^0\)(cmt)
nên ΔCHA đều(Dấu hiệu nhận biết tam giác đều)
b) Xét ΔABC vuông tại A có
\(AC=AB\cdot\tan\widehat{B}\)
\(\Leftrightarrow AC=5\cdot\tan30^0\)
hay \(AC=\dfrac{5\sqrt{3}}{3}cm\)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2=\dfrac{100}{3}\)
hay \(BC=\dfrac{10\sqrt{3}}{3}cm\)
Vậy: \(AC=\dfrac{5\sqrt{3}}{3}cm\); \(BC=\dfrac{10\sqrt{3}}{3}cm\)
Đúng 2
Bình luận (1)
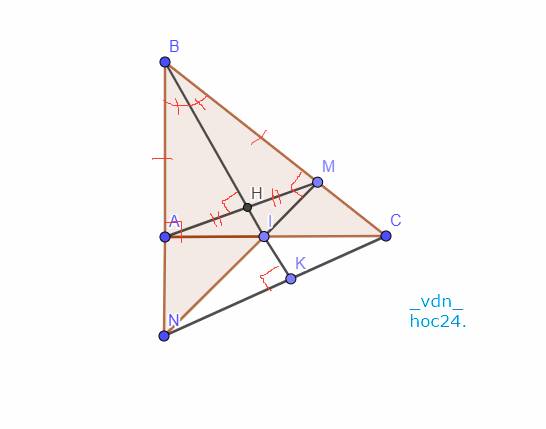
Cho Δ ABC vuông tại A, đường phân giác BI (I ∈ AC). Kẻ IM vuông góc với BC ( M ∈ BC). Gọi N là giao điểm của AB và IM.
a) Chứng minh: Δ ABI =Δ MBI và BI là đường trung trực của đoạn thẳng AM
b) Chứng minh IN = IC
c) Chứng minh BI vuông góc với NC
\(\text{#TNam}\)
`a,`
Xét Tam giác `ABI` và Tam giác `MBI` có:
`\text {BI chung}`
\(\widehat{ABI}=\widehat{MBI} (\text {tia phân giác}\) \(\widehat{ABM} )\)
\(\widehat{BAI}=\widehat{BMI}=90^0\)
`=> \text {Tam giác ABI = Tam giác MBI (ch-gn)}`
`=> BA = BM (\text {2 cạnh tương ứng})`
Gọi `H` là giao điểm của `BI` với `AM`
Xét Tam giác `HAB` và Tam giác `HMB` có:
\(\text{BA = BM (CMT)}\)
\(\widehat{ABH}=\widehat{MBH} (\text {tia phân giác} \widehat{ABM})\)
`\text {BH chung}`
`=> \text {Tam giác HAB = Tam giác HMB (c-g-c)}`
`-> \text {HA = HM (2 cạnh tương ứng)}`
`->`\(\widehat{BHA}=\widehat{BHM} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BHA}+\widehat{BHM}=180^0\)
`->`\(\widehat{BHA}=\widehat{BHM}=\)`180/2=90^0`
`-> \text {BH} \bot \text {AM}`
Ta có: \(\left\{{}\begin{matrix}BH\perp AM\\HA=HM\end{matrix}\right.\)
`->` \(\text{BI là đường trung trực của AM.}\)
`b,`
Xét Tam giác `BAC` và Tam giác `BMN` có:
\(\widehat{B} \) `\text {chung}`
`BA = BM (a)`
\(\widehat{BAC}=\widehat{BMN}=90^0\)
`=> \text {Tam giác BAC = Tam giác BMN (g-c-g)}`
`-> \text {BN = BC (2 cạnh tương ứng)}`
Xét Tam giác `BIN` và Tam giác `BIC` có:
`BN = BC (CMT)`
\(\widehat{NBI}=\widehat{CBI} (\text {tia phân giác} \widehat{NBC})\)
`\text {BI chung}`
`=> \text {Tam giác BIN = Tam giác BIC (c-g-c)}`
`-> \text {IN = IC (2 cạnh tương ứng)}`
`c,`
Gọi `K` là giao điểm của `BI` và `NC`
Xét Tam giác `NBK` và Tam giác `CBK` có:
`BN = BC (CMT)`
\(\widehat{NBK}=\widehat{CBK} (\text {tia phân giác} \widehat{NBC})\)
`\text {BK chung}`
`=> \text {Tam giác NBK = Tam giác CBK (c-g-c)}`
`->`\(\widehat{BKN}=\widehat{BKC} (\text {2 góc tương ứng})\)
Mà `2` góc này nằm ở vị trí kề bù
`->`\(\widehat{BKN}+\widehat{BKC}=180^0\)
`->`\(\widehat{BKN}=\widehat{BKC}=\)`180/2=90^0`
`-> \text {BK} \bot \text {NC}`
`-> \text {BI} \bot \text {NC (đpcm)}`
Đúng 2
Bình luận (0)
Cho ABC cân ở A. Có góc A nhọn Gọi I là trung điểm của BC . Kẻ BD vuông góc với AC tại D , kẻ CE vuông góc với AB tại E . Gọi K là giao điểm của BD và CE .
Chứng minh rằng: a) Δ BCE= ΔCBD
b) Δ BEK= ΔCDK và AK là tia phân giác của góc BAC
c) Ba điểm A,K,I thẳng hàng
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM IN
c) Chứng minh: Góc BIM Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
Đọc tiếp
cho góc nhọn xoy, oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Gọi I là giao điểm của Oz và AB
a, Chứng minh: tam giác OIA = tam giác OIB. Chứng minh Oz và AB
b, Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox, M thuộc Oy). Chứng minh IM = IN
c) Chứng minh: Góc BIM = Góc AIN
d) Chứng minh: MN // AB
ai làm nhanh cho mình cả bài với ạ
THANK YOU SO MUCH
a) Xét tam giác \(OIA\) và tam giác \(OIB\) có:
\(OA=OB\)
\(\widehat{AOI}=\widehat{BOI}\)
\(OI\) cạnh chung
suy ra \(\Delta OIA=\Delta OIB\) (c.g.c)
b) Xét tam giác \(OIN\) và tam giác \(OIM\):
\(\widehat{ION}=\widehat{IOM}\)
\(OI\) cạnh chung
\(\widehat{ONI}=\widehat{OMI}\left(=90^o\right)\)
suy ra \(\Delta OIN=\Delta OIM\) (cạnh huyền - góc nhọn)
\(\Rightarrow IN=IM\)
c) \(\Delta OIA=\Delta OIB\) suy ra \(IA=IB\).
Xét tam giác \(INA\) và tam giác \(IMB\):
\(IA=IB\)
\(\widehat{INA}=\widehat{IMB}\left(=90^o\right)\)
\(IN=IM\)
suy ra \(\Delta INA=\Delta IMB\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\widehat{AIN}=\widehat{BIM}\)
d) \(\Delta OIN=\Delta OIM\) suy ra \(ON=OM\)
suy ra \(\dfrac{ON}{OA}=\dfrac{OM}{OB}\) suy ra \(MN//AB\).
Đúng 0
Bình luận (0)
Cho Δ ABC có AB=AC. Kẻ BD vuông góc AC, CE vuông góc AB (D ϵ AC; E ϵ AB). Gọi O là giao điểm của BD và CE. Chứng minh:
a) Δ ABD = Δ ACE
b) BD = CE
c) Δ AOE = Δ AOD
d) Δ OEB = Δ ODC
e) AO là tia phân giác của góc BAC
mong mọi người giải giúp mình với ạ mình đang cần gấp
Đúng 0
Bình luận (0)
cho góc nhọn xOy, Oz là tia phân giác của góc đó. Trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA =OB . Gọi I là giao điểm của Oz và AB.
a) Chứng minh: . tam giác OIA tam giác OIB Chứng minh Oz vuông góc AB .
b) Từ I kẻ IN vuông góc Ox và IM vuông góc Oy ( N thuộc Ox ,M thuộc Oy) . Chứng minh: IM =IN .
c) Chứng minh: góc BIM = góc AIN .
d)Chứng minh: MN // AB
cho tam giác ABC có góc A= 60 độ. Tia phân giác của góc B cắt AC ở M. Tia phân giác của góc C cắt AB ở N. Gọi I là giao điểm của BM và CN. Chứng minh: IM=IN
CM rằng số B=111...1555...56 là số chính phương {B có n chữ số 1; n-1 chữ số 5; với n thuộc N*} ⋆๖ۣۜGiúp๖ۣۜ Cáiღ
má trên google ko có câu trên => tịt ngok đúng chứ .......... Thế Này mà gọi là ⋆๖ۣۜOLMღ
WOW!
Đúng 0
Bình luận (0)
CM rằng số B=111...1555...56 là số chính phương {B có n chữ số 1; n-1 chữ số 5; với n thuộc N*} ⋆๖ۣۜGiúp๖ۣۜ Cáiღ
má trên google ko có câu trên => tịt ngok đúng chứ .......... Thế Này mà gọi là ⋆๖ۣۜOLMღ
WOW!
Đúng 0
Bình luận (0)
cho tam giác ABC có góc A= 60 độ. Tia phân giác của góc B cắt AC ở M. Tia phân giác của góc C cắt AB ở N. Gọi I là giao điểm của BM và CN. Chứng minh: IM=IN
Dễ dàng c/m được góc EID = 120 độ
--> tứ giác BDIE nội tiếp được.
--> góc IED = IBD và góc IDE = góc IBE (hai góc nội tiếp cùng chắn 1 cung)
mà góc EIB = góc IBD (T/c ba đường phân giác của tam giác)
--> góc IED = góc IDE
--> tam giác IED cân tại I --> IE = ID
dựa vào nhen
Đúng 0
Bình luận (0)


















