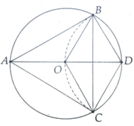
a, HS Tự chứng minh

b, Tính được  C B D ^ = C B O ^ = O B A ^ = 30 0

c, Chứng minh ∆ABC cân tại A có: A B C ^ = 60 0 =>  ∆ABC đều

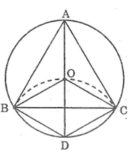
Ta có:

OB = OC = R (vì B, C nằm trên (O; R))

DB = DC = R (vì B, C nằm trên (D; R))

Suy ra: OB = OC = DB = DC

Vậy tứ giác OBDC là hình thoi

Ta có: OB = OC = BD = R

a: Xét tứ giác OBDC có OB=BD=DC=OC=R

nên OBDC là hình thoi

b: Xét ΔOBD có OB=OD=BD(=R)

nên ΔOBD đều

=>\(\widehat{OBD}=60^0\)

OBDC là hình thoi

=>\(\widehat{OCD}=\widehat{OBD}=60^0\)

OBDC là hình thoi

=>\(\widehat{BOC}+\widehat{OBD}=180^0\)

=>\(\widehat{BOC}=180^0-60^0=120^0\)

OBDC là hình thoi

=>\(\widehat{BOC}=\widehat{BDC}=120^0\)

OBDC là hình thoi

=>BC là phân giác của góc OBD

=>\(\widehat{CBD}=\widehat{CBO}=\dfrac{\widehat{OBD}}{2}=\dfrac{60^0}{2}=30^0\)

Xét (O) có

ΔABD nội tiếp

AD là đường kính

Do đó: ΔABD vuông tại B

=>\(\widehat{ABD}=90^0\)

\(\widehat{ABO}+\widehat{OBD}=\widehat{ABD}\)

=>\(\widehat{ABO}+60^0=90^0\)

=>\(\widehat{ABO}=30^0\)

c: Gọi giao điểm của OD và BC là H

OBDC là hình thoi

=>OD vuông góc với BC tại trung điểm của mỗi đường

=>OD\(\perp\)BC tại H và H là trung điểm chung của OD và BC

\(\widehat{ABC}=\widehat{ABO}+\widehat{CBO}=30^0+30^0=60^0\)

Xét ΔABC có

AH là đường cao

AH là đường trung tuyến

Do đó: ΔABC cân tại A

Xét ΔABC cân tại A có \(\widehat{ABC}=60^0\)

nên ΔABC đều